Deep Learning

递归神经网络RNN、LSTM、GRU模型

深度学习

Posted by 月月鸟 on February 4, 2022

1. 递归神经网络（Recurrent Neural Network, RNN）

递归神经网络（Recurrent Neural Network, RNN）是一类专门用于处理序列数据的神经网络，它通过引入循环连接，使得模型能够记住以前的输入信息，并将其应用于当前时刻的预测。RNN 能够捕捉输入数据的时间依赖性，适合处理时间序列、自然语言处理等涉及序列关系的任务。

1.1. RNN的基本概念

RNN的核心思想是利用隐藏状态来存储和传递序列信息。对于时间序列数据，RNN 在每个时间步都会更新隐藏状态，并根据当前的输入和前一时刻的隐藏状态生成新的隐藏状态。其特点是具有记忆功能，可以处理前后关联的信息。

1. 隐藏状态

隐藏状态 ( h_t ) 是当前时间步存储的信息，包含了从前面时刻传递过来的序列信息。它由当前输入 ( x_t ) 和上一时刻的隐藏状态 ( h_{t-1} ) 共同决定： [ h_t = f(W_h h_{t-1} + W_x x_t + b) ] 其中：

  • ( W_h ) 是隐藏状态之间的权重矩阵；
  • ( W_x ) 是输入和隐藏状态之间的权重矩阵；
  • ( b ) 是偏置向量；
  • ( f ) 是一个激活函数（如 tanh 或 ReLU）。

2. 输出

RNN 的输出 ( y_t ) 由当前的隐藏状态决定： [ y_t = g(h_t) ] 其中 ( g ) 是一个激活函数，可以是 softmax 用于分类任务，也可以是线性函数用于回归任务。

1.3 RNN的结构

RNN 可以通过展开的方式理解，如下图所示，在每个时间步，RNN 共享相同的权重，并利用前一个时刻的隐藏状态 ( h_{t-1} ) 和当前输入 ( x_t ) 来计算新的隐藏状态 ( h_t )，然后输出 ( y_t )。

在每个时间步，RNN 使用相同的参数进行计算，这使得模型能够在处理不同长度的序列时保持一致。

1.2。 RNN模拟计算过程

为了更正规地模拟一个 RNN 的计算过程，我们将使用标准的 RNN 公式来进行模拟。RNN 的隐藏状态更新公式为：

[ h_t = f(W_h h_{t-1} + W_x x_t + b) ]

其中：

  • ( h_t ) 是第 ( t ) 个时间步的隐藏状态，
  • ( W_h ) 是隐藏状态的权重矩阵（维度为 ( n \times n )，其中 ( n ) 是隐藏状态的维度），
  • ( W_x ) 是输入到隐藏状态的权重矩阵（维度为 ( n \times m )，其中 ( m ) 是输入的维度），
  • ( x_t ) 是第 ( t ) 个时间步的输入向量（维度为 ( m )），
  • ( b ) 是偏置向量（维度为 ( n )），
  • ( f ) 是非线性激活函数（如 tanh 或 ReLU）。

假设：

  • 我们有 3 个时间步 ( t = 1, 2, 3 )，
  • 输入向量 ( x_t ) 是 2 维向量，
  • 隐藏状态 ( h_t ) 是 2 维向量，
  • 激活函数为 tanh 函数。

设定以下参数：

  • ( W_h = \begin{pmatrix} 0.5 & 0.1 \ 0.3 & 0.7 \end{pmatrix} )（2x2 矩阵），
  • ( W_x = \begin{pmatrix} 0.6 & 0.2 \ 0.4 & 0.8 \end{pmatrix} )（2x2 矩阵），
  • 偏置 ( b = \begin{pmatrix} 0.1 \ 0.2 \end{pmatrix} )（2 维向量），
  • 输入序列 ( x_1 = \begin{pmatrix} 1 \ 0 \end{pmatrix}, x_2 = \begin{pmatrix} 0 \ 1 \end{pmatrix}, x_3 = \begin{pmatrix} 1 \ 1 \end{pmatrix} )，
  • 初始隐藏状态 ( h_0 = \begin{pmatrix} 0 \ 0 \end{pmatrix} )。

激活函数 ( f(x) = \tanh(x) ) 公式为： [ \tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} ]

计算步骤

时间步 1：

  1. 计算 ( W_h h_0 + W_x x_1 + b )： [ W_h h_0 = \begin{pmatrix} 0.5 & 0.1 \ 0.3 & 0.7 \end{pmatrix} \begin{pmatrix} 0 \ 0 \end{pmatrix} = \begin{pmatrix} 0 \ 0 \end{pmatrix} ] [ W_x x_1 = \begin{pmatrix} 0.6 & 0.2 \ 0.4 & 0.8 \end{pmatrix} \begin{pmatrix} 1 \ 0 \end{pmatrix} = \begin{pmatrix} 0.6 \ 0.4 \end{pmatrix} ] [ W_h h_0 + W_x x_1 + b = \begin{pmatrix} 0 \ 0 \end{pmatrix} + \begin{pmatrix} 0.6 \ 0.4 \end{pmatrix} + \begin{pmatrix} 0.1 \ 0.2 \end{pmatrix} = \begin{pmatrix} 0.7 \ 0.6 \end{pmatrix} ]

  2. 应用激活函数 tanh： [ h_1 = \tanh(\begin{pmatrix} 0.7 \ 0.6 \end{pmatrix}) = \begin{pmatrix} \tanh(0.7) \ \tanh(0.6) \end{pmatrix} \approx \begin{pmatrix} 0.604 \ 0.537 \end{pmatrix} ]

时间步 2：

  1. 计算 ( W_h h_1 + W_x x_2 + b )： [ W_h h_1 = \begin{pmatrix} 0.5 & 0.1 \ 0.3 & 0.7 \end{pmatrix} \begin{pmatrix} 0.604 \ 0.537 \end{pmatrix} = \begin{pmatrix} 0.604 \times 0.5 + 0.537 \times 0.1 \ 0.604 \times 0.3 + 0.537 \times 0.7 \end{pmatrix} = \begin{pmatrix} 0.352 + 0.054 \ 0.181 + 0.376 \end{pmatrix} = \begin{pmatrix} 0.406 \ 0.557 \end{pmatrix} ] [ W_x x_2 = \begin{pmatrix} 0.6 & 0.2 \ 0.4 & 0.8 \end{pmatrix} \begin{pmatrix} 0 \ 1 \end{pmatrix} = \begin{pmatrix} 0.2 \ 0.8 \end{pmatrix} ] [ W_h h_1 + W_x x_2 + b = \begin{pmatrix} 0.406 \ 0.557 \end{pmatrix} + \begin{pmatrix} 0.2 \ 0.8 \end{pmatrix} + \begin{pmatrix} 0.1 \ 0.2 \end{pmatrix} = \begin{pmatrix} 0.706 \ 1.557 \end{pmatrix} ]

  2. 应用激活函数 tanh： [ h_2 = \tanh(\begin{pmatrix} 0.706 \ 1.557 \end{pmatrix}) = \begin{pmatrix} \tanh(0.706) \ \tanh(1.557) \end{pmatrix} \approx \begin{pmatrix} 0.608 \ 0.914 \end{pmatrix} ]

时间步 3：

  1. 计算 ( W_h h_2 + W_x x_3 + b )： [ W_h h_2 = \begin{pmatrix} 0.5 & 0.1 \ 0.3 & 0.7 \end{pmatrix} \begin{pmatrix} 0.608 \ 0.914 \end{pmatrix} = \begin{pmatrix} 0.5 \times 0.608 + 0.1 \times 0.914 \ 0.3 \times 0.608 + 0.7 \times 0.914 \end{pmatrix} = \begin{pmatrix} 0.304 + 0.091 \ 0.182 + 0.640 \end{pmatrix} = \begin{pmatrix} 0.395 \ 0.822 \end{pmatrix} ] [ W_x x_3 = \begin{pmatrix} 0.6 & 0.2 \ 0.4 & 0.8 \end{pmatrix} \begin{pmatrix} 1 \ 1 \end{pmatrix} = \begin{pmatrix} 0.6 + 0.2 \ 0.4 + 0.8 \end{pmatrix} = \begin{pmatrix} 0.8 \ 1.2 \end{pmatrix} ] [ W_h h_2 + W_x x_3 + b = \begin{pmatrix} 0.395 \ 0.822 \end{pmatrix} + \begin{pmatrix} 0.8 \ 1.2 \end{pmatrix} + \begin{pmatrix} 0.1 \ 0.2 \end{pmatrix} = \begin{pmatrix} 1.295 \ 2.222 \end{pmatrix} ]

  2. 应用激活函数 tanh： [ h_3 = \tanh(\begin{pmatrix} 1.295 \ 2.222 \end{pmatrix}) = \begin{pmatrix} \tanh(1.295) \ \tanh(2.222) \end{pmatrix} \approx \begin{pmatrix} 0.860 \ 0.976 \end{pmatrix} ]

最终结果

经过 3 个时间步后，隐藏状态的更新为：

  • ( h_1 \approx \begin{pmatrix} 0.604 \ 0.537 \end{pmatrix} )
  • ( h_2 \approx \begin{pmatrix} 0.608 \ 0.914 \end{pmatrix} )
  • ( h_3

\approx \begin{pmatrix} 0.860 \ 0.976 \end{pmatrix} )

每一步中，输入 ( x_t ) 与前一时间步的隐藏状态 ( h_{t-1} ) 被结合在一起通过权重矩阵和偏置进行更新，最后通过非线性激活函数得到新的隐藏状态。

1.3. RNN的类型

根据输入和输出的结构不同，RNN 可以分为以下几类：

  1. 多对一（Many-to-One）：输入是一个序列，输出是一个单独的值。例如，情感分析任务中，输入是一段文本，输出是该文本的情感分类。
  2. 一对多（One-to-Many）：输入是一个单独的值，输出是一个序列。例如，图像描述生成，输入是一张图片，输出是一段描述该图片的句子。
  3. 多对多（Many-to-Many）：输入和输出都是序列。例如，机器翻译任务中，输入是一段句子，输出是翻译后的句子。
  4. 同步多对多（Many-to-Many, Same Length）：输入和输出序列具有相同的长度，例如，视频帧的标签预测。

1.4. RNN的训练与问题

RNN 的训练和传统神经网络类似，通常使用梯度下降法来更新模型参数。然而，由于 RNN 是处理序列的模型，它的反向传播称为“反向传播通过时间（Backpropagation Through Time, BPTT）”。在 BPTT 中，梯度通过多个时间步进行传播，计算所有时间步上的损失，并对模型进行更新。

1.4.1. 梯度消失和梯度爆炸

RNN 在训练时，由于梯度在时间步上进行反向传播，会面临梯度消失或梯度爆炸的问题。当序列长度较长时，梯度逐渐衰减，模型难以捕捉到远距离的依赖关系；另一方面，梯度爆炸会导致梯度过大，模型不稳定。

为了模拟 梯度消失 和 梯度爆炸 的过程，我们需要通过递归神经网络（RNN）中的反向传播过程来解释。以下将会展示一个通过多个时间步的累积计算，逐步观察梯度是如何在计算过程中逐渐减小（梯度消失）或增大（梯度爆炸）的。

梯度消失和梯度爆炸的简单公式

对于时间步 ( t ) 的隐藏状态 ( h_t ) 来说，其递归更新公式为： [ h_t = f(W_h h_{t-1} + W_x x_t + b) ] 如果我们要计算损失 ( L ) 对 ( W_h ) 的梯度，则需要通过反向传播计算链式导数。损失函数 ( L ) 相对于时间步 ( t ) 的梯度为： [ \frac{\partial L}{\partial W_h} = \frac{\partial L}{\partial h_T} \cdot \frac{\partial h_T}{\partial h_{T-1}} \cdot \frac{\partial h_{T-1}}{\partial h_{T-2}} \cdot \ldots \cdot \frac{\partial h_1}{\partial W_h} ] 其中，每一项 ( \frac{\partial h_t}{\partial h_{t-1}} ) 主要受权重矩阵 ( W_h ) 和激活函数的导数影响。

梯度消失的模拟

假设：

  • 我们选择激活函数 ( f ) 为 sigmoid 函数（或 tanh 函数），这些激活函数的导数通常在 ( 0 \leq f’(x) \leq 1 ) 之间。
  • 使用的权重矩阵 ( W_h ) 的数值较小，例如 ( W_h = 0.5 )。

我们来看一个简单的例子，使用递归公式来模拟梯度的衰减。

梯度消失模拟

假设：

  • 时间步 ( t = 1, 2, \ldots, T )
  • 激活函数的导数为 ( f’(x) = 0.5 )（比如 tanh 或 sigmoid 函数在某些输入范围内的典型值）
  • 权重矩阵 ( W_h = 0.5 )

反向传播的计算过程： 每个时间步的梯度可以近似为： [ \frac{\partial h_t}{\partial h_{t-1}} = f’(W_h h_{t-1}) \cdot W_h ] 由于 ( f’(x) = 0.5 ) 且 ( W_h = 0.5 )，我们可以得出每个时间步的梯度为： [ \frac{\partial h_t}{\partial h_{t-1}} = 0.5 \cdot 0.5 = 0.25 ]

那么，随着时间步 ( t ) 增加，最终的梯度是多个时间步梯度的连乘： [ \frac{\partial L}{\partial W_h} = 0.25^{T} ] 当 ( T ) 较大时，梯度呈指数性衰减。例如：

  • ( T = 5 ) 时，梯度为 ( 0.25^5 = 0.000976 )
  • ( T = 10 ) 时，梯度为 ( 0.25^{10} = 0.000000953 )

结论：随着时间步的增加，梯度迅速接近于 0，模型难以学习到远距离的依赖关系，这就是梯度消失现象。

梯度消失的结果：

  • 在较长的序列中，模型逐步“忘记”了早期时间步的信息，因为梯度逐步衰减为接近 0 的值。

梯度爆炸的模拟

我们现在来看看梯度爆炸的情况。

假设：

  • 激活函数仍然为 sigmoid 或 tanh 函数，但这次我们设定权重矩阵 ( W_h ) 的数值较大，例如 ( W_h = 2 )。
  • 激活函数的导数 ( f’(x) ) 仍然为 ( 0.5 )。

梯度爆炸模拟

每个时间步的梯度近似为： [ \frac{\partial h_t}{\partial h_{t-1}} = f’(W_h h_{t-1}) \cdot W_h ] 由于 ( W_h = 2 ) 和 ( f’(x) = 0.5 )，每个时间步的梯度为： [ \frac{\partial h_t}{\partial h_{t-1}} = 0.5 \cdot 2 = 1 ] 这时候，每一层的梯度将不会变小，而是保持 1。

如果我们进一步增加 ( W_h )，例如 ( W_h = 3 )，则每一层的梯度为： [ \frac{\partial h_t}{\partial h_{t-1}} = 0.5 \cdot 3 = 1.5 ]

随着时间步增加，最终梯度是多个时间步梯度的连乘： [ \frac{\partial L}{\partial W_h} = 1.5^{T} ] 当 ( T ) 较大时，梯度呈指数性增长。例如：

  • ( T = 5 ) 时，梯度为 ( 1.5^5 = 7.59 )
  • ( T = 10 ) 时，梯度为 ( 1.5^{10} = 57.67 )

结论：随着时间步的增加，梯度迅速增大，甚至可能达到无法控制的程度。这就是梯度爆炸现象。

梯度爆炸的结果：

  • 梯度在每一时间步上都迅速放大，导致参数更新的幅度过大，模型训练变得不稳定，甚至可能无法收敛。

总结

  • 梯度消失：当权重较小且激活函数导数趋近于 0 时，梯度会呈指数衰减，随着时间步的增加，梯度趋近于 0，导致模型难以捕捉长时间步的依赖关系。
  • 梯度爆炸：当权重较大时，梯度会呈指数增长，导致训练过程中梯度过大，模型难以收敛，甚至数值会溢出。

这两个问题在标准 RNN 中非常常见，尤其是在处理长序列时。因此，引入了 LSTM 和 GRU 等改进模型来解决这些问题。

1.4.2. 短期依赖问题

短期依赖问题是递归神经网络（RNN）在处理长序列数据时的一种局限性，具体表现为 RNN 更擅长处理序列中相对较近的时间步之间的依赖关系，而在捕捉远距离的、较长时间步之间的依赖关系时会遇到困难。这种现象与梯度消失问题紧密相关。

RNN 是通过在时间步之间共享隐藏状态来捕捉序列数据的时间依赖性。随着时间步的增加，早期输入的信息通过隐藏状态逐步传递给后续时间步。然而，当序列长度较长时，早期时间步的信息很容易在隐藏状态的多次更新过程中被“稀释”或“遗忘”，最终难以对后续时间步的输出产生有效影响。这就导致了 RNN 更容易依赖短期的信息，忽视远距离的依赖。

1.5. 改进的 RNN 结构

1. LSTM（Long Short-Term Memory）

LSTM 是一种专门设计用于解决 RNN 梯度消失问题的改进版本。LSTM 引入了“遗忘门”、“输入门”和“输出门”来控制信息的流动，从而能够有效地记住较长的序列信息。

  • 遗忘门：决定哪些信息应该被遗忘。
  • 输入门：决定哪些信息应该被写入当前状态。
  • 输出门：决定从当前状态输出哪些信息。

LSTM 通过这些门控机制，能够更好地捕捉长期依赖关系。

2. GRU（Gated Recurrent Unit）

GRU 是 LSTM 的简化版本，它将 LSTM 的遗忘门和输入门合并成了一个“更新门”，并保留了类似的门控机制。GRU 相比 LSTM 计算更为高效，性能也相当。

1.6. 应用场景

RNN 及其变种在处理序列数据的任务中表现优异，常见的应用场景包括：

  • 自然语言处理（NLP）：如文本分类、机器翻译、语言模型等。
  • 语音识别：RNN 能够处理语音信号中的时序依赖关系，应用于语音识别和生成。
  • 时间序列预测：如股票预测、天气预报等。
  • 视频分析：RNN 可以处理视频中的序列帧信息，用于动作识别或场景理解。

2. LSTM（Long Short-Term Memory）

LSTM（Long Short-Term Memory）是一种特殊的递归神经网络（RNN），专门用于处理序列数据，尤其是具有长时间依赖性的任务。LSTM 是为了克服传统 RNN 中梯度消失和梯度爆炸问题而设计的，特别适用于长序列数据的建模。

2.1. LSTM的结构：

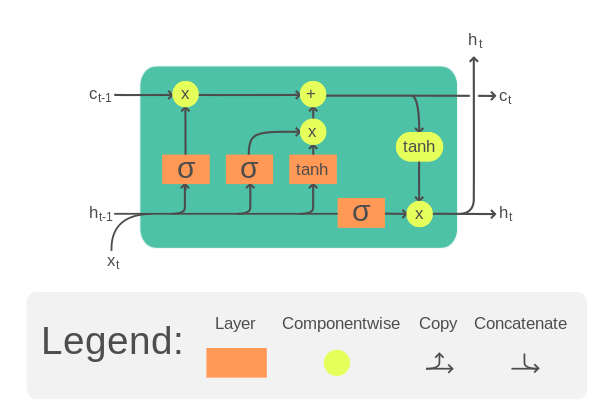
LSTM 通过引入“记忆细胞”（memory cell）和一组“门”（gates）来实现更好的长期依赖处理。每个 LSTM 单元（cell）包含三个门，它们用于控制信息的流动：

  1. 遗忘门（Forget Gate）：决定哪些信息需要从记忆单元中遗忘或丢弃。
  2. 输入门（Input Gate）：决定哪些新的信息会被存入记忆单元中。
  3. 输出门（Output Gate）：决定当前时刻的隐藏状态会输出什么信息。

LSTM 通过这些门结构，能够选择性地保留或丢弃信息，从而有效地捕捉长期依赖关系，而不像传统 RNN 那样在长时间序列数据中容易发生梯度消失或爆炸。

2.2. LSTM的公式：

在每个时间步 ( t )，LSTM 的状态更新公式如下：

  1. 遗忘门： [ f_t = \sigma(W_f \cdot [h_{t-1}, x_t] + b_f) ] ( f_t ) 控制记忆单元中哪些信息被遗忘，( W_f ) 和 ( b_f ) 是权重矩阵和偏置项，( h_{t-1} ) 是上一个时间步的隐藏状态，( x_t ) 是当前输入。

  2. 输入门： [ i_t = \sigma(W_i \cdot [h_{t-1}, x_t] + b_i) ] ( i_t ) 控制哪些信息被加入到记忆单元中。

  3. 候选记忆单元： [ \tilde{C}t = \tanh(W_C \cdot [h{t-1}, x_t] + b_C) ] 这是候选的新信息，准备被加入到记忆单元。

  4. 更新记忆单元： [ C_t = f_t * C_{t-1} + i_t * \tilde{C}_t ] 记忆单元 ( C_t ) 是基于遗忘门和输入门的组合，整合了历史信息和新输入。

  5. 输出门： [ o_t = \sigma(W_o \cdot [h_{t-1}, x_t] + b_o) ] ( o_t ) 决定当前时间步的隐藏状态 ( h_t )。

  6. 隐藏状态更新： [ h_t = o_t * \tanh(C_t) ] 隐藏状态 ( h_t ) 是当前时刻要输出的结果。

2.3.LSTM的应用：

LSTM 常用于以下任务：

  • 自然语言处理（NLP）：如机器翻译、情感分析等。
  • 时间序列预测：如股票价格预测、气象预测等。
  • 语音识别：处理语音信号中的时间序列数据。
  • 视频处理：从视频帧中提取连续的时间信息。

2.4. 简单的例子计算

LSTM 在捕捉长时间序列中的依赖关系方面非常有效，常用于各种需要建模序列数据的领域。我们可以通过一个简单的例子来展示 LSTM 的计算过程。假设我们有以下输入序列 ( x = [x_1, x_2, x_3] )，并且我们将 LSTM 的各个参数简化为标量操作。

1. 初始化：

我们首先初始化以下状态：

  • 隐藏状态 ( h_0 = 0 )
  • 记忆单元 ( C_0 = 0 )

假设每个门的权重和偏置都是固定的值（为了简单说明）：

  • 遗忘门权重 ( W_f = 0.5 )，偏置 ( b_f = 0 )
  • 输入门权重 ( W_i = 0.5 )，偏置 ( b_i = 0 )
  • 候选记忆单元权重 ( W_C = 0.5 )，偏置 ( b_C = 0 )
  • 输出门权重 ( W_o = 0.5 )，偏置 ( b_o = 0 )

每个门使用的是 sigmoid 函数 ( \sigma(x) = \frac{1}{1 + e^{-x}} )，而候选记忆单元使用的是 ( \tanh ) 函数。

2. 第一步计算（ ( t = 1 ) 时）：

输入： ( x_1 = 1 )

遗忘门：

[ f_1 = \sigma(W_f \cdot h_0 + b_f) = \sigma(0.5 \cdot 0 + 0) = 0.5 ]

输入门：

[ i_1 = \sigma(W_i \cdot h_0 + b_i) = \sigma(0.5 \cdot 0 + 0) = 0.5 ]

候选记忆单元：

[ \tilde{C}_1 = \tanh(W_C \cdot h_0 + b_C) = \tanh(0.5 \cdot 0 + 0) = 0 ]

更新记忆单元：

[ C_1 = f_1 \cdot C_0 + i_1 \cdot \tilde{C}_1 = 0.5 \cdot 0 + 0.5 \cdot 0 = 0 ]

输出门：

[ o_1 = \sigma(W_o \cdot h_0 + b_o) = \sigma(0.5 \cdot 0 + 0) = 0.5 ]

隐藏状态更新：

[ h_1 = o_1 \cdot \tanh(C_1) = 0.5 \cdot \tanh(0) = 0 ]

3. 第二步计算（ ( t = 2 ) 时）：

输入： ( x_2 = 2 )

遗忘门：

[ f_2 = \sigma(W_f \cdot h_1 + b_f) = \sigma(0.5 \cdot 0 + 0) = 0.5 ]

输入门：

[ i_2 = \sigma(W_i \cdot h_1 + b_i) = \sigma(0.5 \cdot 0 + 0) = 0.5 ]

候选记忆单元：

[ \tilde{C}_2 = \tanh(W_C \cdot h_1 + b_C) = \tanh(0.5 \cdot 0 + 0) = 0 ]

更新记忆单元：

[ C_2 = f_2 \cdot C_1 + i_2 \cdot \tilde{C}_2 = 0.5 \cdot 0 + 0.5 \cdot 0 = 0 ]

输出门：

[ o_2 = \sigma(W_o \cdot h_1 + b_o) = \sigma(0.5 \cdot 0 + 0) = 0.5 ]

隐藏状态更新：

[ h_2 = o_2 \cdot \tanh(C_2) = 0.5 \cdot \tanh(0) = 0 ]

4. 第三步计算（ ( t = 3 ) 时）：

输入： ( x_3 = 3 )

遗忘门：

[ f_3 = \sigma(W_f \cdot h_2 + b_f) = \sigma(0.5 \cdot 0 + 0) = 0.5 ]

输入门：

[ i_3 = \sigma(W_i \cdot h_2 + b_i) = \sigma(0.5 \cdot 0 + 0) = 0.5 ]

候选记忆单元：

[ \tilde{C}_3 = \tanh(W_C \cdot h_2 + b_C) = \tanh(0.5 \cdot 0 + 0) = 0 ]

更新记忆单元：

[ C_3 = f_3 \cdot C_2 + i_3 \cdot \tilde{C}_3 = 0.5 \cdot 0 + 0.5 \cdot 0 = 0 ]

输出门：

[ o_3 = \sigma(W_o \cdot h_2 + b_o) = \sigma(0.5 \cdot 0 + 0) = 0.5 ]

隐藏状态更新：

[ h_3 = o_3 \cdot \tanh(C_3) = 0.5 \cdot \tanh(0) = 0 ]

总结：

经过三步的计算，隐藏状态 ( h_1, h_2, h_3 ) 都是 0。这个简单的例子

3. GRU（Gated Recurrent Unit，门控循环单元）

是RNN的一种变体，类似于LSTM，但相比之下结构更简单。GRU 模型主要用于解决传统 RNN 中长时间依赖时的梯度消失问题。相比 LSTM，GRU 去掉了 LSTM 中的记忆单元（Cell State）和输出门，而是通过两个门（更新门和重置门）来控制信息流动，因而计算更为高效。

GRU的结构：

GRU 的核心在于两个门控机制：更新门（Update Gate） 和 重置门（Reset Gate）。这两个门分别决定是否将之前的信息保留，或者重置。

  1. 更新门（Update Gate）：控制当前时间步的信息与先前时间步的信息之间的融合程度，类似于 LSTM 的输入门和遗忘门的结合体。
  2. 重置门（Reset Gate）：控制遗忘机制，即决定丢弃多少过去的记忆，用以生成候选的隐藏状态。

GRU的公式：

与 LSTM 类似，GRU 的计算也分为几个步骤：

  1. 更新门： [ z_t = \sigma(W_z \cdot [h_{t-1}, x_t]) ] 其中，( z_t ) 是更新门的输出，( W_z ) 是权重矩阵，( h_{t-1} ) 是上一时刻的隐藏状态，( x_t ) 是当前的输入，( \sigma ) 是 sigmoid 函数。

  2. 重置门： [ r_t = \sigma(W_r \cdot [h_{t-1}, x_t]) ] ( r_t ) 是重置门的输出，控制是否要忘记之前的隐藏状态。

  3. 候选隐藏状态： [ \tilde{h}t = \tanh(W_h \cdot [r_t * h{t-1}, x_t]) ] 其中，( \tilde{h}_t ) 是当前的候选隐藏状态，( r_t ) 决定了是否重置先前的隐藏状态，( \tanh ) 函数用于生成新的候选隐藏状态。

  4. 隐藏状态更新： [ h_t = z_t * h_{t-1} + (1 - z_t) * \tilde{h}t ] 最终的隐藏状态 ( h_t ) 是更新门 ( z_t ) 结合了上一时刻的隐藏状态 ( h{t-1} ) 和当前的候选状态 ( \tilde{h}_t ) 所产生的。

GRU与LSTM的比较：

  • 结构简单：GRU 有两个门，而 LSTM 有三个门和一个额外的记忆单元，因此 GRU 计算更简单，训练速度更快。
  • 性能相似：在很多任务中，GRU 和 LSTM 的性能接近，但由于 GRU 更简单，在某些任务上可能会表现得更好，特别是在计算资源有限的情况下。
  • 长时间依赖：两者都擅长处理长时间依赖的问题，但由于 LSTM 具有独立的记忆单元，它可能在处理某些复杂的时间序列任务时更具优势。

GRU的应用：

与 LSTM 类似，GRU 也被广泛应用于序列数据建模的任务中，包括：

  • 自然语言处理（NLP）中的文本生成、机器翻译、语音识别。
  • 时间序列预测，如金融市场数据分析。
  • 视频处理中的帧间关系建模。

GRU 的优点在于它比 LSTM 更加简洁、速度更快，但仍能够保留很好的性能表现。

CATALOG
    FEATURED TAGS
    Algorithm Data Structure Machine Learning Deep Learning NLP Computer Vision
    FRIENDS