1. 二分查找
二分查找(binary search)是一种基于分治策略的高效搜索算法。它利用数据的有序性,每次迭代将搜索范围缩小一半,直到找到目标元素或搜索区间为空为止。
问题描述
给定一个长度为 n 的数组 nums,其中元素按从小到大的顺序排列且不重复。请查找并返回元素 target 在该数组中的索引。若数组不包含该元素,则返回 -1。示例如图所示。
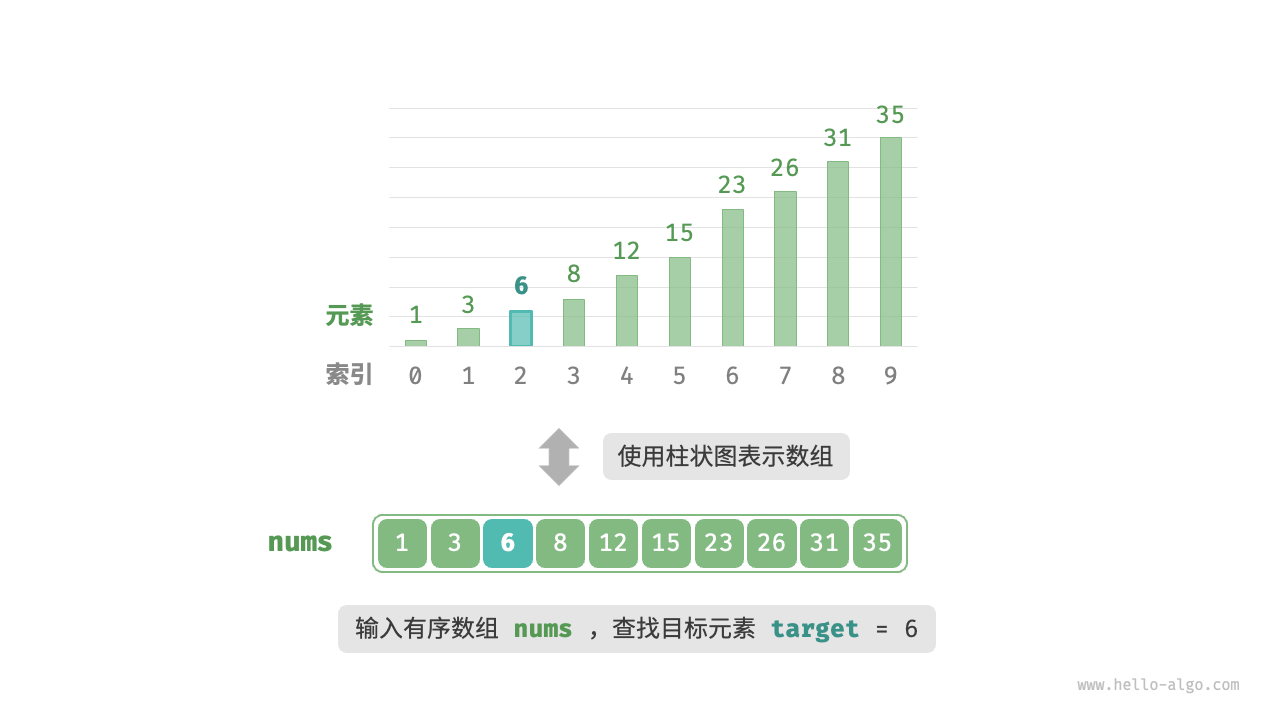
二分查找示例数据
如图所示,我们先初始化指针 i 和 j,分别指向数组首元素和尾元素,代表搜索区间 [i, j]。注意,中括号表示闭区间,包含边界值本身。

接下来,循环执行以下两步:
- 计算中点索引
m,其中m = (i + j) // 2(//表示向下取整操作)。 - 判断
nums[m]和target的大小关系,分为以下三种情况:- 当
nums[m] < target时,说明target在区间[m+1, j]中,因此执行i = m + 1。 - 当
nums[m] > target时,说明target在区间[i, m-1]中,因此执行j = m - 1。 - 当
nums[m] == target时,说明找到了target,返回索引m。
- 当
若数组不包含目标元素,搜索区间最终会缩小为空。此时返回 -1。
注意事项
由于 i 和 j 都是 int 类型,因此在其他语言中,i + j 可能会超出 int 类型的取值范围。为了避免大数越界,通常采用公式 m = i + (j - i) // 2 来计算中点。
Python 代码实现
def binary_search(nums: list[int], target: int) -> int:
"""二分查找(双闭区间)"""
# 初始化双闭区间 [0, n-1] ,即 i, j 分别指向数组首元素、尾元素
i, j = 0, len(nums) - 1
# 循环,当搜索区间为空时跳出(当 i > j 时为空)
while i <= j:
# 理论上 Python 的数字可以无限大(取决于内存大小),无须考虑大数越界问题
m = (i + j) // 2 # 计算中点索引 m
if nums[m] < target:
i = m + 1 # 此情况说明 target 在区间 [m+1, j] 中
elif nums[m] > target:
j = m - 1 # 此情况说明 target 在区间 [i, m-1] 中
else:
return m # 找到目标元素,返回其索引
return -1 # 未找到目标元素,返回 -1
时间复杂度和空间复杂度
- 时间复杂度:O(log n) —— 每次迭代搜索区间缩小一半,因此循环次数为 log n。
- 空间复杂度:O(1) —— 仅使用了常数大小的空间存储指针
i和j。
1.1 区间表示方法
除了上述双闭区间 [i, j],常见的区间表示还有“左闭右开”区间 [i, j),即左边界包含自身,右边界不包含自身。在这种表示下,区间 [i, j) 在 i = j 时为空。
基于左闭右开区间的二分查找实现如下:
def binary_search_lcro(nums: list[int], target: int) -> int:
"""二分查找(左闭右开区间)"""
# 初始化左闭右开区间 [0, n) ,即 i, j 分别指向数组首元素、尾元素+1
i, j = 0, len(nums)
# 循环,当搜索区间为空时跳出(当 i = j 时为空)
while i < j:
m = (i + j) // 2 # 计算中点索引 m
if nums[m] < target:
i = m + 1 # 此情况说明 target 在区间 [m+1, j) 中
elif nums[m] > target:
j = m # 此情况说明 target 在区间 [i, m) 中
else:
return m # 找到目标元素,返回其索引
return -1 # 未找到目标元素,返回 -1
图展示了两种区间定义的区别。相比之下,“双闭区间”表示法在缩小区间的操作中更加对称,因此不容易出错,因此更推荐使用“双闭区间”的写法。
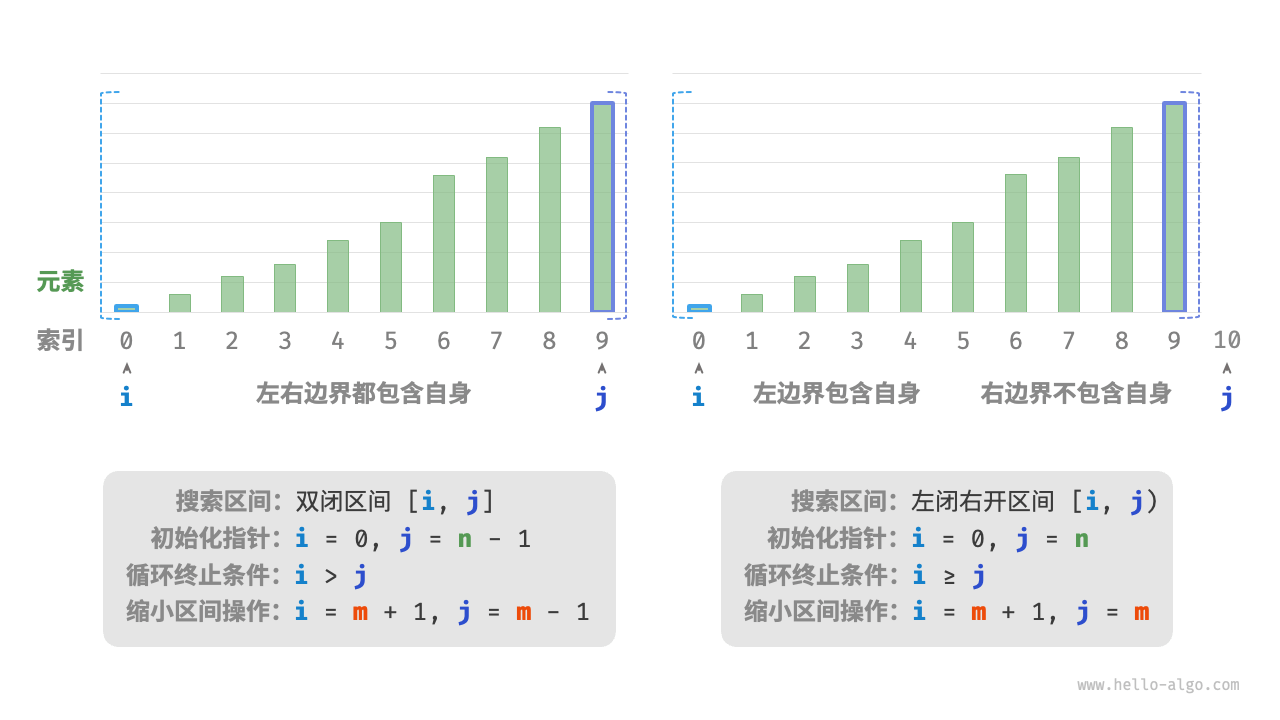
1.2 优点与局限性
二分查找在时间和空间方面都有较好的性能:
优点:
- 时间效率高:对数阶的时间复杂度在大数据量下优势明显。例如,当数据量为
n时,线性查找需要n轮循环,而二分查找仅需 log n 轮循环。 - 无须额外空间:与需要额外空间的搜索算法(如哈希查找)相比,二分查找更加节省空间。
局限性:
- 仅适用于有序数据:若输入数据无序,则需要先进行排序,这将带来更高的时间复杂度,通常为 O(n log n)。
- 仅适用于数组:二分查找需要跳跃式(非连续地)访问元素,这在链表中效率较低,因此不适用于链表或基于链表的数据结构。
- 小数据量下线性查找更佳:在小数据量下,线性查找的性能可能优于二分查找,因为每轮线性查找只需一次判断,而二分查找需要多次操作。
这样,二分查找在适合的场景中能够提供高效的查找功能,但其应用条件也相对严格。
2. 二分查找插入点
二分查找不仅可以用于搜索目标元素,还可以用于解决变种问题,比如查找目标元素的插入位置。
2.1 无重复元素的情况
问题描述
给定一个长度为 n 的有序数组 nums 和一个元素 target,数组中不存在重复元素。现将 target 插入数组 nums 中,并保持其有序性。若数组中已存在 target,则将其插入到相等元素的左侧。请返回插入后 target 在数组中的索引。示例如图 10-4 所示。
二分查找插入点示例数据
图 10-4 展示了二分查找插入点的示例数据。
为了复用上一节的二分查找代码,我们需要回答以下两个问题:
问题一:当数组中包含 target 时,插入点的索引是否是该元素的索引?
题目要求将 target 插入到相等元素的左侧,因此新插入的 target 替换了原来 target 的位置。这意味着当数组包含 target 时,插入点的索引就是该 target 的索引。
问题二:当数组中不存在 target 时,插入点是哪个元素的索引?
在二分查找过程中,当 nums[m] < target 时,指针 i 向右移动,这意味着 i 在靠近大于或等于 target 的元素;当 nums[m] > target 时,指针 j 向左移动,靠近小于或等于 target 的元素。
因此,二分查找结束时,i 指向首个大于 target 的元素,j 指向首个小于 target 的元素。当数组中不包含 target 时,插入索引为 i。代码如下:
def binary_search_insertion_simple(nums: list[int], target: int) -> int:
"""二分查找插入点(无重复元素)"""
i, j = 0, len(nums) - 1 # 初始化双闭区间 [0, n-1]
while i <= j:
m = (i + j) // 2 # 计算中点索引 m
if nums[m] < target:
i = m + 1 # target 在区间 [m+1, j] 中
elif nums[m] > target:
j = m - 1 # target 在区间 [i, m-1] 中
else:
return m # 找到 target ,返回插入点 m
# 未找到 target ,返回插入点 i
return i
2.2 存在重复元素的情况
问题描述
在上一题的基础上,假设数组可能包含重复元素。其余条件不变。
如果数组中存在多个 target,普通二分查找只能返回其中一个 target 的索引,无法确定该元素的左侧和右侧有多少个 target。题目要求将目标元素插入到最左侧,因此我们需要查找数组中最左边的 target 索引。初步思路如下:
- 执行二分查找,找到任意一个
target的索引,记为m。 - 从索引
m开始,向左线性遍历,找到最左侧的target并返回其索引。
虽然此方法可行,但包含线性查找,因此时间复杂度为 O(n)。在数组中存在大量重复 target 的情况下,效率较低。
为了提升效率,可以扩展二分查找的代码。图 10-6 展示了具体步骤。在每轮迭代中,先计算中点索引 m,然后判断 target 和 nums[m] 的大小关系,分为以下情况:
- 当
nums[m] < target或nums[m] > target时,尚未找到target,继续采用普通二分查找的缩小区间操作,使指针i和j靠近target。 - 当
nums[m] == target时,意味着小于target的元素在[i, m-1]区间内,因此将区间缩小到[i, m-1]使j = m - 1,从而靠近最左侧的target。
循环完成后,i 指向最左边的 target,j 指向首个小于 target 的元素,因此插入点索引为 i。代码如下:
def binary_search_insertion(nums: list[int], target: int) -> int:
"""二分查找插入点(存在重复元素)"""
i, j = 0, len(nums) - 1 # 初始化双闭区间 [0, n-1]
while i <= j:
m = (i + j) // 2 # 计算中点索引 m
if nums[m] < target:
i = m + 1 # target 在区间 [m+1, j] 中
elif nums[m] > target:
j = m - 1 # target 在区间 [i, m-1] 中
else:
j = m - 1 # 首个小于 target 的元素在区间 [i, m-1] 中
# 返回插入点 i
return i
提示
以上代码均采用“双闭区间”的写法。读者可尝试实现“左闭右开”区间的版本。
总结来看,二分查找的本质是为指针 i 和 j 设定搜索目标,目标可能是一个具体元素(如 target),也可能是一个范围(如小于 target 的元素)。在不断循环中,i 和 j 逐渐逼近预设目标,最终找到答案或停止搜索。
3. 二分查找边界
3.1 查找左边界
问题描述
给定一个长度为 n 的有序数组 nums,其中可能包含重复元素。请返回数组中最左边的 target 元素的索引。若数组中不包含该元素,则返回 -1。
回忆二分查找插入点的方法,在搜索完成后,指针 i 指向最左边的 target,因此查找插入点本质上就是查找最左边的 target 索引。
为实现查找左边界,可以直接复用查找插入点的函数。注意,数组中可能不包含 target,这种情况下可能会出现以下两种情况:
- 插入点索引
i越界。 - 元素
nums[i]与target不相等。
当遇到上述情况时,直接返回 -1。代码如下:
def binary_search_left_edge(nums: list[int], target: int) -> int:
"""二分查找最左一个 target"""
# 等价于查找 target 的插入点
i = binary_search_insertion(nums, target)
# 未找到 target ,返回 -1
if i == len(nums) or nums[i] != target:
return -1
# 找到 target ,返回索引 i
return i
3.2 查找右边界
如何查找最右边的 target 呢?最直接的方法是修改二分查找的代码,在 nums[m] == target 的情况下调整指针的收缩操作。不过,这里我们介绍两种更巧妙的方法。
方法 1:复用查找左边界
我们可以利用查找最左边元素的函数来查找最右边的元素。具体方法是将查找最右边的 target 转化为查找最左边的 target + 1。
如图 10-7 所示,查找完成后,指针 i 指向最左边的 target + 1(如果存在),而指针 j 指向最右边的 target,因此返回 j 即可。
将查找右边界转化为查找左边界
注意,返回的插入点是 i,因此需要将其减 1,从而得到 j 的值:
def binary_search_right_edge(nums: list[int], target: int) -> int:
"""二分查找最右一个 target"""
# 转化为查找最左一个 target + 1
i = binary_search_insertion(nums, target + 1)
# j 指向最右一个 target ,i 指向首个大于 target 的元素
j = i - 1
# 未找到 target ,返回 -1
if j == -1 or nums[j] != target:
return -1
# 找到 target ,返回索引 j
return j
方法 2:转化为查找元素
当数组中不包含 target 时,最终 i 和 j 会分别指向首个大于和首个小于 target 的元素。
因此,如图 10-8 所示,我们可以通过构造一个数组中不存在的元素来查找左右边界:
- 查找最左边的
target:可以转化为查找target - 0.5,并返回指针i。 - 查找最右边的
target:可以转化为查找target + 0.5,并返回指针j。
将查找边界转化为查找元素
以下几点需要注意:
- 给定数组不包含小数,这意味着我们无需处理相等的情况。
- 因为该方法引入了小数,因此需要将函数中的变量
target改为浮点数类型(Python 中无须特别处理)。
通过这些方法,我们能够高效地找到数组中目标元素的最左边和最右边索引,进一步拓展了二分查找的应用。
4. 哈希优化策略
在算法题中,为了降低时间复杂度,我们常常通过将线性查找替换为哈希查找。下面通过一个具体的算法题来加深对这种优化策略的理解。
问题描述
给定一个整数数组 nums 和一个目标元素 target,请在数组中搜索“和”为 target 的两个元素,并返回它们的数组索引。返回任意一个解即可。
4.1 线性查找:以时间换空间
最简单的做法是直接遍历所有可能的组合。图 10-9 所示为这一方法的过程:我们使用两层循环,在每轮中判断两个整数的和是否等于 target,若相等,则返回它们的索引。
线性查找求解两数之和
图 10-9 展示了线性查找的示例流程。
代码如下:
def two_sum_brute_force(nums: list[int], target: int) -> list[int]:
"""方法一:暴力枚举"""
# 两层循环,时间复杂度为 O(n^2)
for i in range(len(nums) - 1):
for j in range(i + 1, len(nums)):
if nums[i] + nums[j] == target:
return [i, j]
return []
这种方法的时间复杂度为 O(n^2),空间复杂度为 O(1),在处理大数据量时非常耗时。
4.2 哈希查找:以空间换时间
为了提高效率,我们可以借助一个哈希表,将数组元素和它们的索引作为键值对。遍历数组的每一轮时,执行以下步骤(如图 10-10 所示):
- 检查哈希表中是否存在
target - nums[i],若存在,则返回这两个元素的索引。 - 将当前元素
nums[i]和它的索引i添加到哈希表中。
辅助哈希表求解两数之和
图 10-10 展示了哈希查找求解的示例流程。
实现代码如下,仅需单层循环即可:
def two_sum_hash_table(nums: list[int], target: int) -> list[int]:
"""方法二:辅助哈希表"""
# 辅助哈希表,空间复杂度为 O(n)
dic = {}
# 单层循环,时间复杂度为 O(n)
for i in range(len(nums)):
if target - nums[i] in dic:
return [dic[target - nums[i]], i]
dic[nums[i]] = i
return []
通过使用哈希查找,时间复杂度从 O(n^2) 降至 O(n),极大地提升了算法的运行效率。
虽然此方法需要维护一个额外的哈希表,因此空间复杂度为 O(n),但整体上时空效率更为均衡,是解决这类问题的最优解法。
5. 重识搜索算法
搜索算法(searching algorithm)用于在数据结构(例如数组、链表、树或图)中查找一个或多个满足特定条件的元素。根据实现思路,搜索算法大致可以分为以下两类:
- 遍历搜索:通过遍历数据结构来定位目标元素,例如数组、链表、树和图的遍历。
- 基于数据特性搜索:利用数据组织结构或先验信息,实现高效查找,例如二分查找、哈希查找和二叉搜索树查找。
这些搜索算法我们在前面章节中已有所涉及,因此对它们并不陌生。在本节中,我们将从更加系统的视角重新审视搜索算法。
5.1 暴力搜索
暴力搜索通过遍历数据结构的每个元素来定位目标元素:
- 线性搜索:适用于数组和链表等线性数据结构。从数据结构的一端开始,逐个访问元素,直到找到目标元素或到达末端仍未找到。
- 广度优先搜索(BFS)和深度优先搜索(DFS):适用于图和树的两种遍历策略。BFS从初始节点逐层搜索,由近及远地访问各节点;DFS从初始节点沿着一条路径走到底,再回溯尝试其他路径,直到遍历完整个数据结构。
暴力搜索的优点是简单且通用,无需对数据进行预处理或借助额外的数据结构。然而,暴力搜索的时间复杂度为 O(n),其中 n 为元素数量,因此在数据量较大时性能较差。
5.2 自适应搜索
自适应搜索利用数据的特定属性(如有序性)来优化搜索过程,更高效地定位目标元素:
- 二分查找:利用数据的有序性实现高效查找,仅适用于数组。
- 哈希查找:利用哈希表将数据和目标建立键值对映射,实现快速查找。
- 树查找:在特定树结构(如二叉搜索树)中,通过比较节点值快速定位目标元素。
这类算法效率高,时间复杂度可以达到 O(log n) 甚至 O(1)。然而,使用这些算法往往需要对数据进行预处理。例如,二分查找需要对数组排序,哈希查找和树查找需要借助额外的数据结构,且维护这些结构也需要额外的时间和空间开销。
提示
自适应搜索算法通常被称为查找算法,主要用于在特定数据结构中快速检索目标元素。
5.3 搜索方法选取
对于大小为 n 的一组数据,可以使用线性搜索、二分查找、树查找、哈希查找等多种方法搜索目标元素。各个方法的工作原理如图 10-11 所示。
多种搜索策略
表 10-1 对比了这些查找算法的效率和特点。
| 搜索方法 | 查找元素 | 插入元素 | 删除元素 | 额外空间 | 数据预处理 | 数据是否有序 |
|---|---|---|---|---|---|---|
| 线性搜索 | O(n) | O(n) | O(n) | O(1) | 无 | 无序 |
| 二分查找 | O(log n) | O(n) | O(n) | O(1) | 排序 | 有序 |
| 树查找 | O(log n) | O(log n) | O(log n) | O(n) | 建树 | 有序 |
| 哈希查找 | O(1) | O(1) | O(1) | O(n) | 建哈希表 | 无序 |
选择搜索算法时需考虑数据规模、搜索性能需求、数据的查询和更新频率等因素。
-
线性搜索
适用于无需预处理的场景,且通用性好。假如只需一次查询,其他方法的数据预处理时间可能比线性搜索更长。
适合体量较小的数据,此时时间复杂度对效率影响较小。
适合数据更新频率较高的场景,因为无需额外维护数据结构。 -
二分查找
适合大数据量场景,效率表现稳定,最差时间复杂度为 O(log n)。
不适合过大的数据量,因为存储数组需要连续的内存空间。
不适合高频增删数据场景,因维护有序数组开销较大。 -
哈希查找
适用于对查询性能要求高的场景,平均时间复杂度为 O(1)。
不适合需要有序数据或范围查找的场景,因哈希表无法维护数据的有序性。
对哈希函数和冲突处理策略的依赖较高,有性能劣化风险。
不适合超大数据量,因为哈希表需要额外空间来减少冲突,从而提升查询性能。 -
树查找
适用于海量数据,因树节点分散存储。
适合需要维护有序数据或范围查找的场景。
在持续增删节点过程中,二叉搜索树可能倾斜,导致时间复杂度恶化至 O(n)。
若使用 AVL 树或红黑树,所有操作在 O(log n) 效率下稳定运行,但维护树平衡会增加额外开销。
通过以上分析,可以根据具体应用场景选择合适的搜索算法,实现高效的元素查找。