Data Structure

算法与数据结构 (Algorithms and Data Structures)

图(10)

Posted by 月月鸟 on September 27, 2021

1. 图的基本概念

图（graph）是一种非线性数据结构，由顶点（vertex）和边（edge）组成。我们可以将图 $G$ 抽象地表示为一组顶点 $V$ 和一组边 $E$ 的集合。以下示例展示了一个包含 5 个顶点和 7 条边的图。

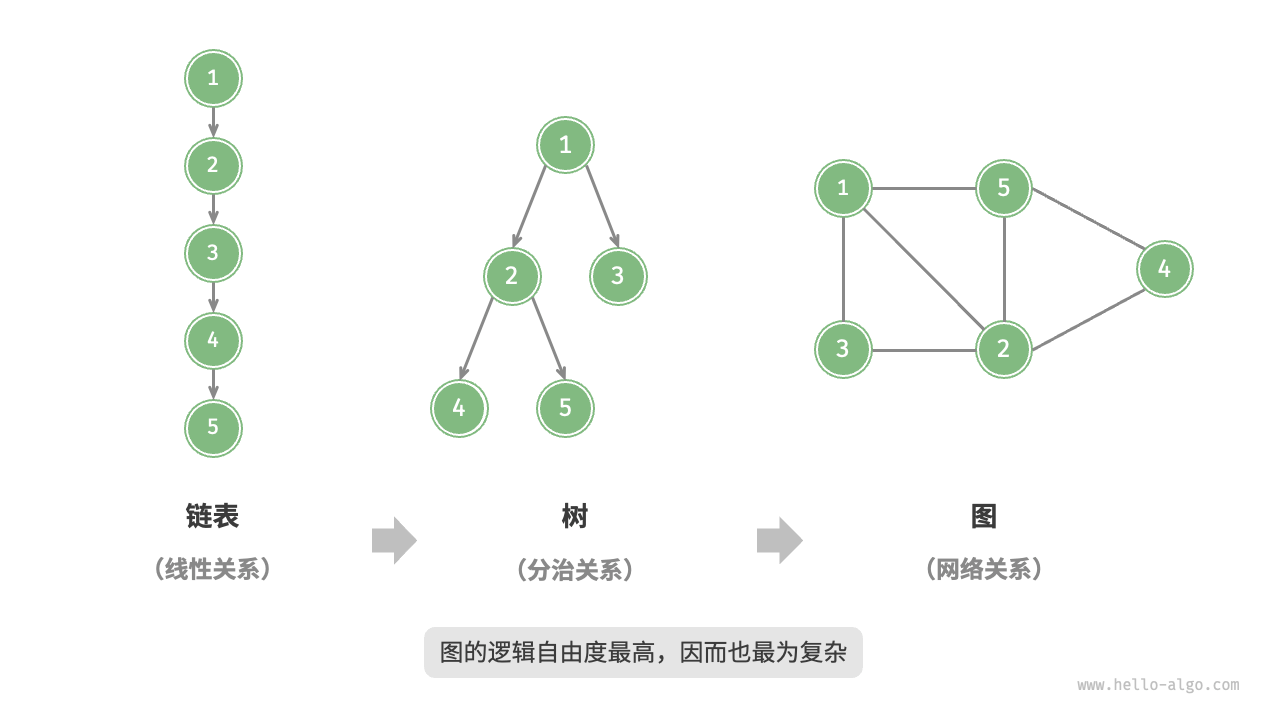
\[\begin{aligned} V & = \{ 1, 2, 3, 4, 5 \} \\ E & = \{ (1,2), (1,3), (1,5), (2,3), (2,4), (2,5), (4,5) \} \\ G & = \{ V, E \} \\ \end{aligned}\]

如果我们将顶点看作节点，将边看作连接节点的引用（或指针），则图可以视为从链表扩展而来的数据结构。如下图所示，相较于线性结构（链表）和分支结构（树），网络结构（图）的自由度更高，因此更为复杂。

链表、树、图之间的关系

2. 图的常见类型与术语

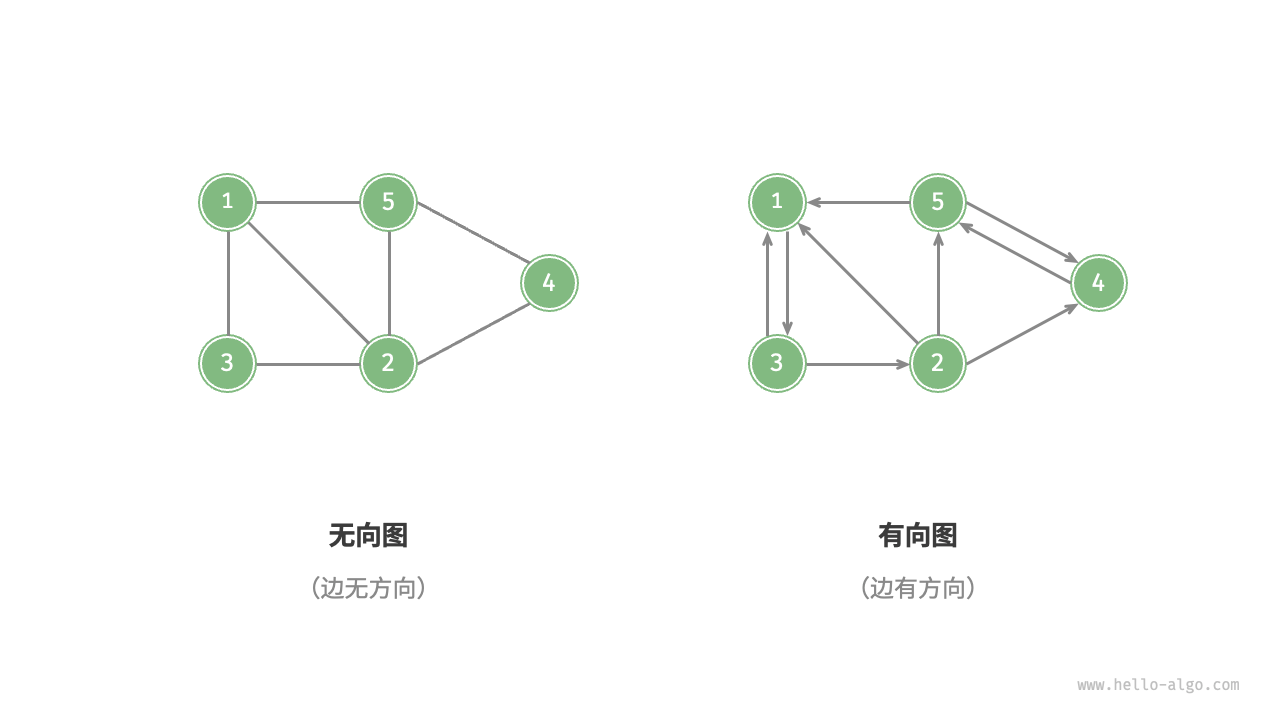
根据边的方向性，图可分为无向图（Undirected Graph）和有向图（Directed Graph），如下图所示。

  • 无向图：边表示两个顶点之间的双向连接关系。例如，社交应用中的“好友关系”。
  • 有向图：边具有方向性，即 $A \rightarrow B$ 与 $A \leftarrow B$ 是独立的。例如，社交媒体中的“关注”与“被关注”关系。

有向图与无向图

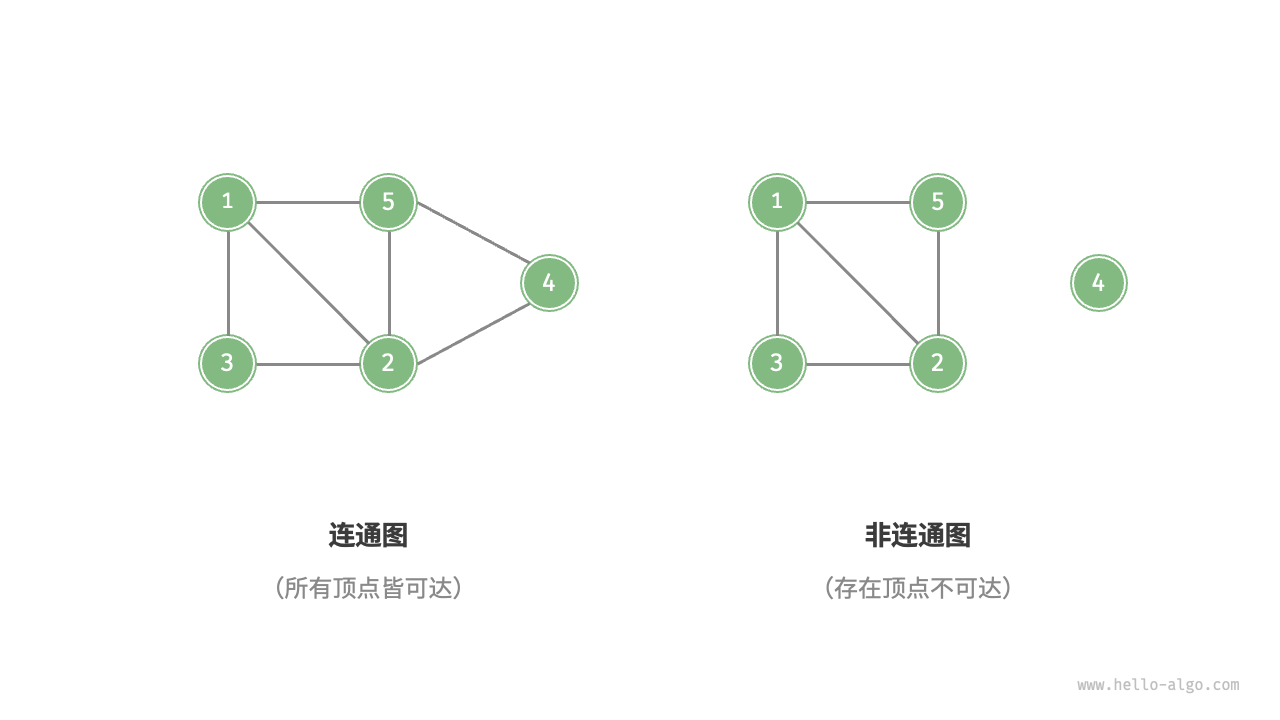
根据所有顶点是否连通，图可分为连通图（Connected Graph）和非连通图（Disconnected Graph），如下图所示。

  • 连通图：从任一顶点出发，可以到达其余任意顶点。
  • 非连通图：至少存在一个顶点无法从其他顶点到达。

连通图与非连通图

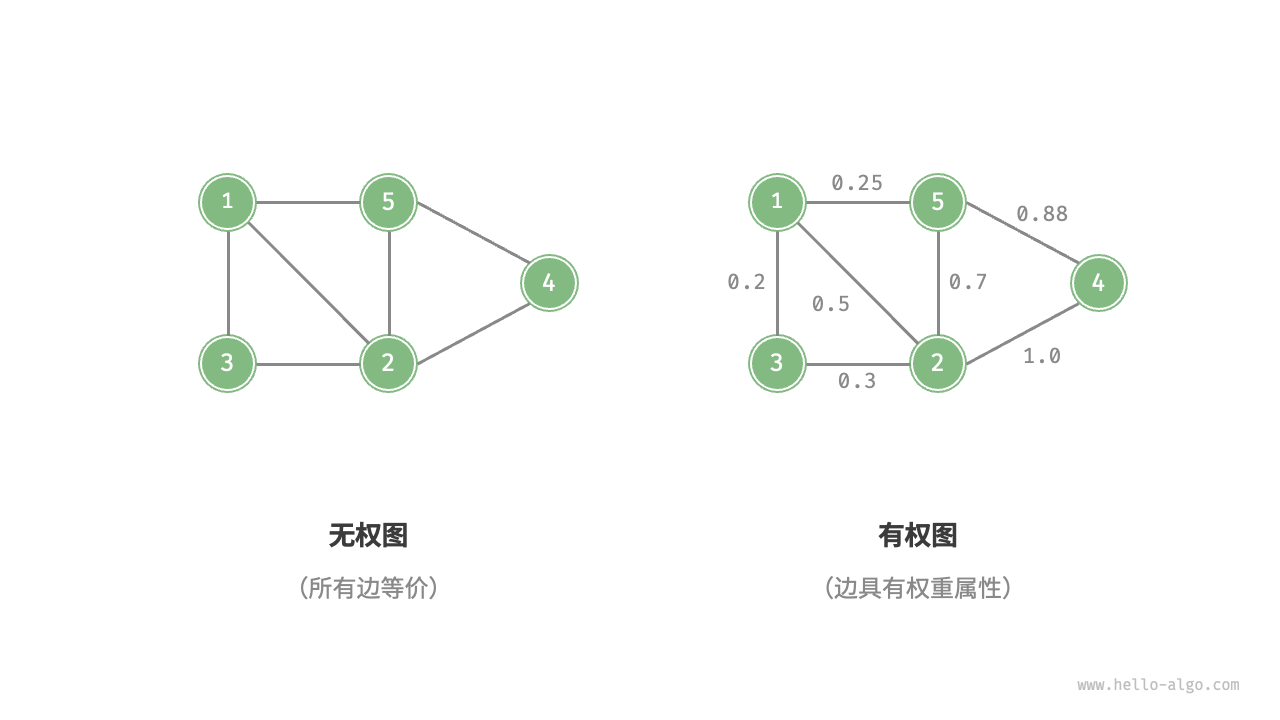
图的边还可以赋予权重，从而得到有权图（Weighted Graph）。例如，在多人在线游戏中，系统根据共同游戏时间计算玩家之间的“亲密度”，这种亲密度网络就可以用有权图来表示。

有权图与无权图

图数据结构中常见的术语包括：

  • 邻接（Adjacency）：当两顶点之间存在边相连时，称这两顶点为邻接顶点。在上图中，顶点 1 的邻接顶点为顶点 2、3、5。
  • 路径（Path）：从顶点 A 到顶点 B 经过的边构成的序列称为从 A 到 B 的路径。在上图中，边序列 1-5-2-4 是从顶点 1 到顶点 4 的一条路径。
  • 度（Degree）：一个顶点拥有的边数。在有向图中，入度（In-degree）表示指向该顶点的边数，出度（Out-degree）表示从该顶点指出的边数。

3. 图的表示方法

图常用的表示方法有“邻接矩阵”和“邻接表”。以下以无向图为例进行说明。

3.1. 邻接矩阵

设图的顶点数为 $n$，邻接矩阵（Adjacency Matrix）用一个 $n \times n$ 的矩阵表示图。矩阵的行和列代表顶点，矩阵的元素表示顶点之间的边，用 $1$ 表示有边相连，用 $0$ 表示无边相连。

如下图所示，设邻接矩阵为 $M$，顶点列表为 $V$，矩阵元素 $M[i, j] = 1$ 表示顶点 $V[i]$ 和顶点 $V[j]$ 之间存在边，反之则表示两顶点之间无边。

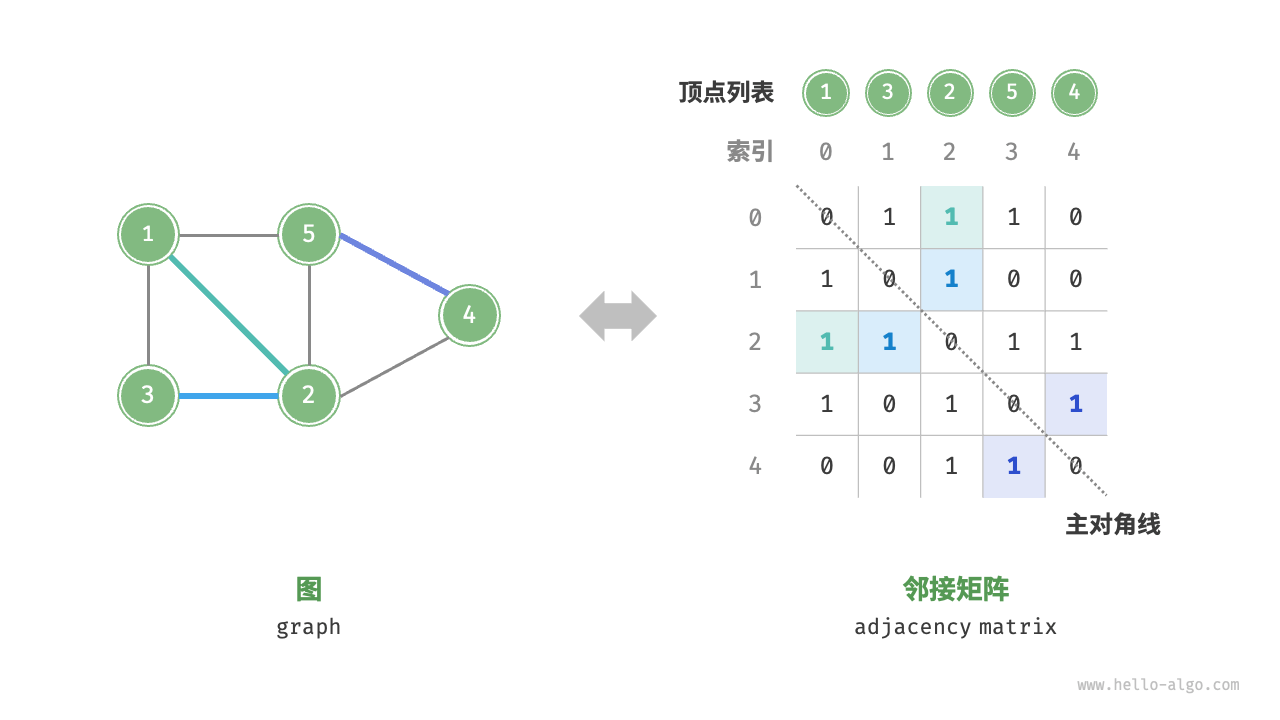
图的邻接矩阵表示

邻接矩阵具有以下特性：

  • 顶点不能与自身相连，因此邻接矩阵的主对角线元素没有意义。
  • 对于无向图，矩阵关于主对角线对称。
  • 将邻接矩阵的 $1$ 和 $0$ 替换为权重，可以表示有权图。

使用邻接矩阵表示图时，可以直接访问矩阵元素获取边信息，增删查改操作效率高，时间复杂度为 $O(1)$。但由于矩阵的空间复杂度为 $O(n^2)$，内存占用较多。

3.2. 邻接表

邻接表（Adjacency List）用 $n$ 个链表表示图，链表的节点表示顶点。第 $i$ 个链表对应顶点 $i$，其中存储了该顶点的所有邻接顶点（与该顶点相连的顶点）。下图展示了一个使用邻接表存储的图的示例。

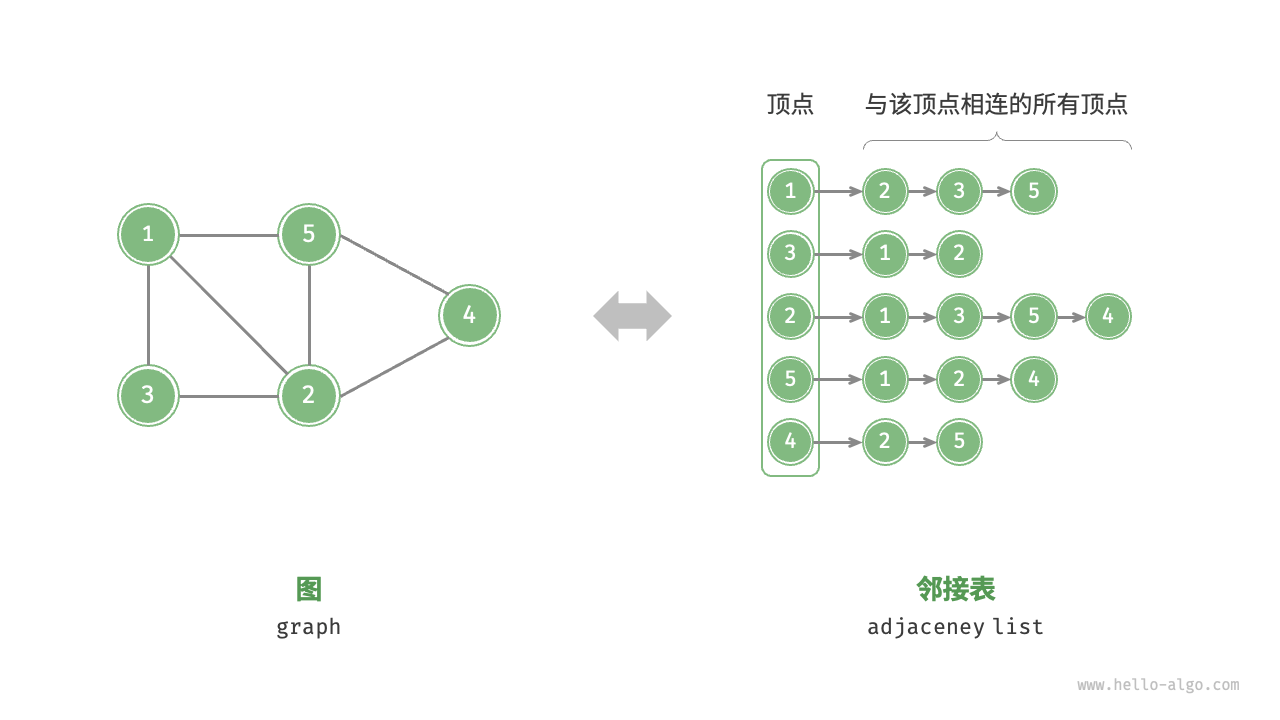
图的邻接表表示

邻接表只存储实际存在的边，因此空间利用更为高效，尤其当边的数量远小于 $n^2$ 时。然而，在邻接表中查找边时需要遍历链表，时间效率不如邻接矩阵。

观察上图，邻接表的结构与哈希表中的“链式地址”非常相似，可以使用类似的方法优化效率。例如，当链表较长时，可以将链表转化为 AVL 树或红黑树，将查找效率优化至 $O(\log n)$；或者将链表转换为哈希表，将时间复杂度降至 $O(1)$。

4. 图的常见应用

下表展示了图在现实生活中的一些常见应用场景，相应的问题通常可以通过图计算方法来解决。

表 1: 现实生活中常见的图应用

场景 顶点 边 图计算问题
社交网络 用户 好友关系 潜在好友推荐
地铁线路 站点 站点间的连通性 最短路线推荐
太阳系 星体 星体间的万有引力作用 行星轨道计算

5. 图的基础操作

图的基础操作是图论中的常见操作，主要涉及图的创建、节点和边的操作、图的遍历等。在无向图、有向图和加权图中，这些操作的细节可能会有所不同。下面将详细介绍图的基础操作。

1. 图的表示方法

  • 邻接矩阵：二维数组，表示图中节点之间的连接关系。
    • 若节点 i 和节点 j 之间有边，则 matrix[i][j] = 1（无向图为对称矩阵，有向图非对称）。
    • 若没有边，则 matrix[i][j] = 0。
  • 邻接表：每个节点都有一个列表，列出它相邻的节点。
    • 每个节点的列表包含与该节点相连的所有其他节点。

2. 图的基本操作

图的基本操作包括节点、边的添加和删除，检查连接关系，获取节点或边的信息等。

a. 创建图

  • 邻接矩阵表示： 初始化一个 N x N 的矩阵，其中 N 是节点数量，所有初始值为 0。

    # Initialize an empty adjacency matrix for 5 nodes
N = 5
adj_matrix = [[0] * N for _ in range(N)]

  • 邻接表表示： 使用字典或列表来表示图。

    # Initialize an empty adjacency list for 5 nodes
adj_list = {i: [] for i in range(5)}

b. 添加节点

在邻接矩阵中，节点的数量是固定的，因此添加节点意味着需要扩展矩阵。

  • 邻接矩阵：扩展矩阵的大小。

    # Add a new node to an adjacency matrix (expand matrix)
new_node = [0] * (N + 1)
adj_matrix.append(new_node)
for row in adj_matrix:
    row.append(0)

  • 邻接表：直接在邻接表中添加一个新节点。

    # Add a new node to an adjacency list
adj_list[N] = []

c. 添加边

  • 邻接矩阵：更新矩阵中的对应位置为 1，若是无向图，需要对称更新。

    # Add an edge between node 0 and node 1 in an adjacency matrix
adj_matrix[0][1] = 1  # For directed graph
adj_matrix[1][0] = 1  # For undirected graph

  • 邻接表：在节点对应的列表中添加邻接的节点。

    # Add an edge between node 0 and node 1 in an adjacency list
adj_list[0].append(1)  # For directed graph
adj_list[1].append(0)  # For undirected graph

d. 删除边

  • 邻接矩阵：将矩阵对应位置的值设置为 0。

    # Remove an edge between node 0 and node 1 in an adjacency matrix
adj_matrix[0][1] = 0  # For directed graph
adj_matrix[1][0] = 0  # For undirected graph

  • 邻接表：从节点的邻接列表中移除对应的邻接节点。

    # Remove an edge between node 0 and node 1 in an adjacency list
adj_list[0].remove(1)  # For directed graph
adj_list[1].remove(0)  # For undirected graph

e. 检查两节点是否相连

  • 邻接矩阵：检查矩阵中对应位置是否为 1。

    # Check if node 0 and node 1 are connected in an adjacency matrix
connected = adj_matrix[0][1] == 1

  • 邻接表：检查一个节点的邻接列表中是否存在另一个节点。

    # Check if node 0 and node 1 are connected in an adjacency list
connected = 1 in adj_list[0]

f. 获取节点的所有邻接节点

  • 邻接矩阵：遍历矩阵的行，找出所有值为 1 的位置。

    # Get all adjacent nodes of node 0 in an adjacency matrix
neighbors = [i for i, val in enumerate(adj_matrix[0]) if val == 1]

  • 邻接表：直接返回节点的邻接列表。

    # Get all adjacent nodes of node 0 in an adjacency list
neighbors = adj_list[0]

3. 图的遍历

图的遍历主要有两种方式：广度优先搜索（BFS） 和 深度优先搜索（DFS），前面我们已经实现了BFS的代码，下面是DFS的代码。

广度优先搜索（BFS）代码实现

from collections import deque

# BFS function using adjacency matrix
def bfs_adj_matrix(graph_matrix, start):
    visited = set()  # Set to track visited nodes
    queue = deque([start])  # Initialize the queue with the start node
    result = []  # To store the order of visited nodes
    
    while queue:
        node = queue.popleft()
        
        if node not in visited:
            visited.add(node)
            result.append(node)
            
            # Traverse the adjacency matrix row for the current node
            for neighbor, is_connected in enumerate(graph_matrix[node]):
                if is_connected == 1 and neighbor not in visited:
                    queue.append(neighbor)
    
    return result

# Example graph as an adjacency matrix
# The graph is:
#    A  B  C  D  E  F
# A [0, 1, 1, 0, 0, 0]
# B [0, 0, 0, 1, 1, 0]
# C [0, 0, 0, 0, 0, 1]
# D [0, 0, 0, 0, 0, 0]
# E [0, 0, 0, 0, 0, 1]
# F [0, 0, 0, 0, 0, 0]

graph_matrix = [
    [0, 1, 1, 0, 0, 0],  # A
    [0, 0, 0, 1, 1, 0],  # B
    [0, 0, 0, 0, 0, 1],  # C
    [0, 0, 0, 0, 0, 0],  # D
    [0, 0, 0, 0, 0, 1],  # E
    [0, 0, 0, 0, 0, 0],  # F
]

# Starting BFS from node 0 (which corresponds to 'A')
bfs_order = bfs_adj_matrix(graph_matrix, 0)
# Convert indices back to node names for better understanding
node_names = ['A', 'B', 'C', 'D', 'E', 'F']
bfs_order_named = [node_names[i] for i in bfs_order]

print("BFS Traversal Order:", bfs_order_named)

深度优先搜索（DFS）

# DFS using adjacency list
def dfs(graph, node, visited=None):
    if visited is None:
        visited = set()
    
    # Mark the current node as visited
    visited.add(node)
    print(node, end=" ")  # Process the current node
    
    # Recur for all the vertices adjacent to this vertex
    for neighbor in graph[node]:
        if neighbor not in visited:
            dfs(graph, neighbor, visited)

# Example graph as adjacency list
graph = {
    'A': ['B', 'C'],
    'B': ['D', 'E'],
    'C': ['F'],
    'D': [],
    'E': ['F'],
    'F': []
}

# Start DFS traversal from node 'A'
dfs(graph, 'A')

总结

图的基础操作包括：

  1. 创建图（邻接矩阵或邻接表）
  2. 添加、删除节点和边
  3. 检查节点是否连接
  4. 获取节点的邻接节点
  5. 图的遍历（DFS和BFS）

这些操作是图论问题的基础，可以应用于更复杂的图算法中，例如最短路径、最小生成树等。如果你有具体的图操作需求或需要深入了解某一部分，随时告诉我！

CATALOG
    FEATURED TAGS
    Algorithm Data Structure Machine Learning Deep Learning NLP Computer Vision LLM
    FRIENDS