1. 基本概念

堆（Heap）是一种特殊的树形数据结构，满足以下特性：

1. 完全二叉树：堆是一棵完全二叉树，也就是说，除了最后一层，其余各层的节点都是满的，且最后一层的节点都集中在最左边。

2. 堆性质：

   • 最大堆（Max-Heap）：对于堆中的每个节点，父节点的值都大于或等于其子节点的值。换句话说，根节点包含最大值。
   • 最小堆（Min-Heap）：对于堆中的每个节点，父节点的值都小于或等于其子节点的值。换句话说，根节点包含最小值。

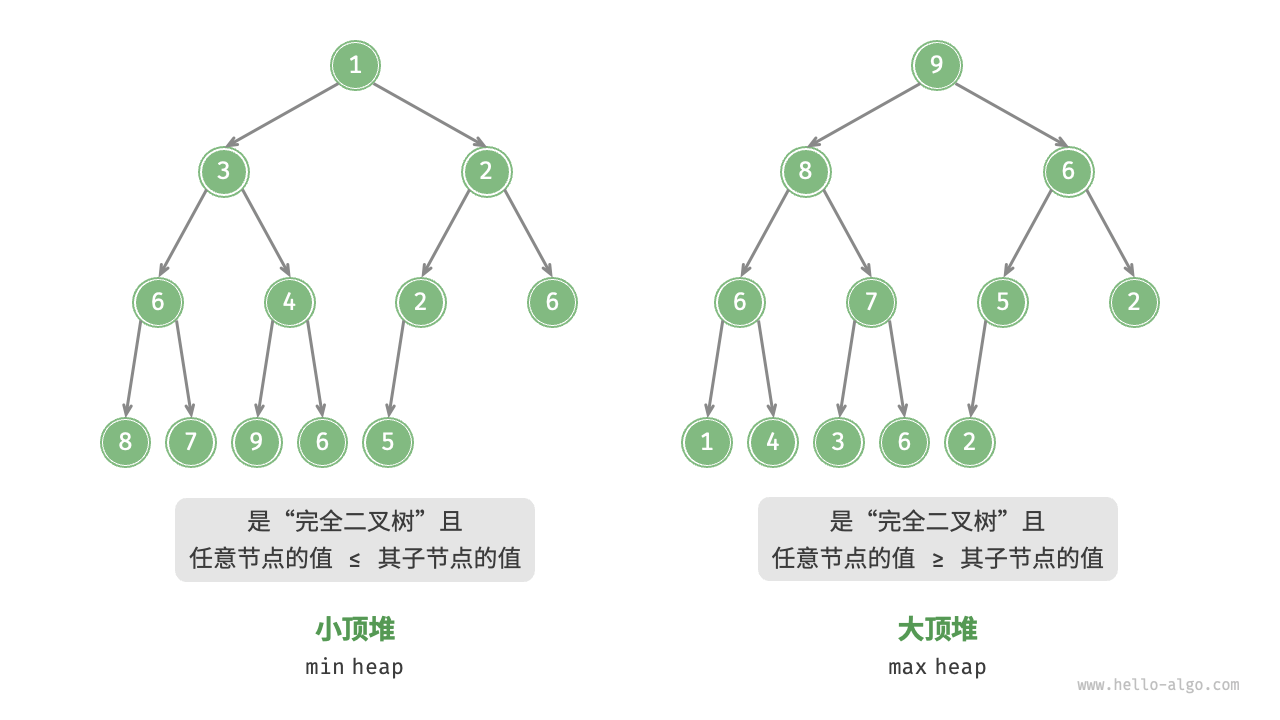
堆是完全二叉树的一种特例，具备以下特点：

• 最底层节点从左到右依次填充，其他层的节点则被完全填满。
• 在堆中，根节点被称为“堆顶”，而底层最右侧的节点被称为“堆底”。
• 对于大顶堆（或小顶堆）而言，堆顶元素（即根节点）的值是所有节点中最大（或最小）的。

2. 堆的基本操作

1. 插入操作：
   • 插入新元素时，首先将其添加到堆的末尾（完全二叉树的最后一个位置）。
   • 然后通过“上浮”操作，将新元素逐步与其父节点交换位置，直到堆性质满足为止。
   • 上浮操作的时间复杂度是 (O(\log n))，因为堆的高度为 (\log n)。

class MaxHeap:
    def __init__(self):
        self.heap = []

    def push(self, value):
        self.heap.append(value)  # 添加到堆的末尾
        self._heapify_up(len(self.heap) - 1)

    def _heapify_up(self, index):
        parent = (index - 1) // 2
        # 上浮操作：如果当前节点比父节点大，就交换位置
        while index > 0 and self.heap[index] > self.heap[parent]:
            self.heap[index], self.heap[parent] = self.heap[parent], self.heap[index]
            index = parent
            parent = (index - 1) // 2

    def __str__(self):
        return str(self.heap)

# 示例
heap = MaxHeap()
heap.push(3)
heap.push(1)
heap.push(6)
heap.push(5)
heap.push(9)
heap.push(8)
print(heap)  # 输出: [9, 5, 8, 1, 3, 6]

1. 删除操作（通常是删除堆顶元素）：
   • 删除堆顶元素后，用堆的最后一个元素替换堆顶。
   • 然后通过“下沉”操作，将新堆顶元素逐步与其子节点交换位置，直到堆性质满足为止。
   • 下沉操作的时间复杂度也是 (O(\log n))。

class MaxHeap:
    def __init__(self):
        self.heap = []

    def push(self, value):
        self.heap.append(value)
        self._heapify_up(len(self.heap) - 1)

    def pop(self):
        if len(self.heap) == 0:
            return None
        if len(self.heap) == 1:
            return self.heap.pop()

        root_value = self.heap[0]
        # 将最后一个元素移到堆顶
        self.heap[0] = self.heap.pop()
        # 下沉操作
        self._heapify_down(0)
        return root_value

    def _heapify_up(self, index):
        parent = (index - 1) // 2
        while index > 0 and self.heap[index] > self.heap[parent]:
            self.heap[index], self.heap[parent] = self.heap[parent], self.heap[index]
            index = parent
            parent = (index - 1) // 2

    def _heapify_down(self, index):
        left = 2 * index + 1
        right = 2 * index + 2
        largest = index

        if left < len(self.heap) and self.heap[left] > self.heap[largest]:
            largest = left
        if right < len(self.heap) and self.heap[right] > self.heap[largest]:
            largest = right
        if largest != index:
            self.heap[index], self.heap[largest] = self.heap[largest], self.heap[index]
            self._heapify_down(largest)

    def __str__(self):
        return str(self.heap)

# 示例
heap = MaxHeap()
heap.push(3)
heap.push(1)
heap.push(6)
heap.push(5)
heap.push(9)
heap.push(8)
print(heap.pop())  # 输出: 9
print(heap)  # 输出: [8, 5, 6, 1, 3]

1. 构建堆：
   • 给定一个无序数组，可以通过“自底向上”的方式构建堆，即从最后一个非叶节点开始，依次对每个节点执行下沉操作。
   • 这种构建堆的方式称为Heapify，时间复杂度为 (O(n))。 ```python class MaxHeap: def init(self): self.heap = []

   def build_heap(self, array): self.heap = array start_index = len(self.heap) // 2 - 1 # 最后一个非叶节点 for i in range(start_index, -1, -1): self._heapify_down(i)

   def _heapify_down(self, index): left = 2 * index + 1 right = 2 * index + 2 largest = index

    if left < len(self.heap) and self.heap[left] > self.heap[largest]:
        largest = left
    if right < len(self.heap) and self.heap[right] > self.heap[largest]:
        largest = right
    if largest != index:
        self.heap[index], self.heap[largest] = self.heap[largest], self.heap[index]
        self._heapify_down(largest)
   

   def str(self): return str(self.heap)

示例

array = [3, 1, 6, 5, 9, 8] heap = MaxHeap() heap.build_heap(array) print(heap) # 输出: [9, 5, 8, 1, 3, 6] ```

3. 堆实际应用

1. 优先级队列：
   • 堆最常用于实现优先级队列。优先级队列是一种数据结构，每个元素都有一个优先级，元素的处理顺序根据其优先级确定。在优先级队列中，堆可以高效地支持插入和删除操作，并能够在对数时间内提供最大（或最小）优先级的元素。
2. 堆排序：
   • 堆排序是一种基于堆的数据结构的排序算法。通过构建最大堆（或最小堆），将最大（或最小）元素移到堆顶，然后逐步将堆顶元素取出，并重新调整堆，直到所有元素排序完成。堆排序的时间复杂度为 O(n log n)，是一种不需要额外空间的原地排序算法。
3. 图算法：
   • 在图算法中，堆常用于实现 Dijkstra 算法和 Prim 算法。Dijkstra 算法用于求解单源最短路径问题，Prim 算法用于求解最小生成树。在这些算法中，堆可以高效地支持优先级的提取和更新操作，从而提高算法的性能。
4. 动态数据流处理：
   • 在需要处理动态数据流时，例如流量监控或在线分析，堆可以用于维护数据流中的前 k 大元素或最小元素。通过使用最大堆或最小堆，可以在实时数据流中有效地提取所需的元素。
5. 内存管理：
   • 堆还可以用于实现内存管理中的一些功能，如动态内存分配。许多内存分配器使用堆数据结构来跟踪可用的内存块，从而高效地分配和释放内存。

• Previous
  算法与数据结构 (Algorithms and Data Structures)
• Next
  算法与数据结构 (Algorithms and Data Structures)