1. 基本概念

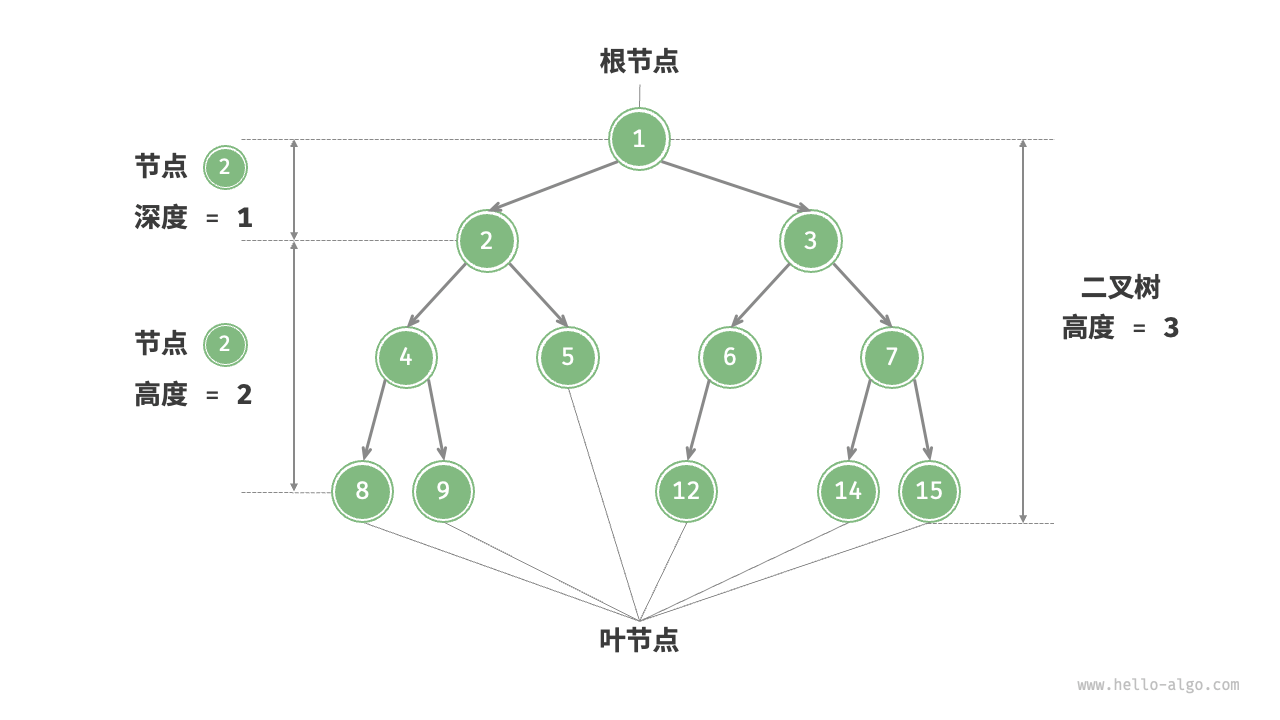
二叉树（binary tree）是一种非线性数据结构，用于表示“祖先”与“后代”之间的层级关系，体现了“一分为二”的分治逻辑。与链表类似，二叉树的基本单元是节点，每个节点包含一个值、一个指向左子节点的引用和一个指向右子节点的引用。每个节点都有两个引用，分别指向左子节点和右子节点，而该节点则被称为这两个子节点的父节点。给定一个二叉树的节点时，该节点的左子节点及其以下节点形成的树称为左子树（left subtree），右子节点及其以下节点形成的树称为右子树（right subtree）。二叉树是一种树形数据结构，每个节点最多有两个子节点：左子节点和右子节点。二叉树广泛应用于计算机科学中，例如用于构建表达式树、决策树和二叉搜索树等。

节点（Node）：
- 值（Value）：节点中存储的数据。
- 左子节点（Left Child）：当前节点的左边子树的根节点。
- 右子节点（Right Child）：当前节点的右边子树的根节点。
根节点（root node）：位于二叉树顶层的节点，没有父节点。
叶节点（leaf node）：没有子节点的节点，其两个指针均指向 None。
边（edge）：连接两个节点的线段，即节点之间的引用（指针）。
节点所在的层（level）：从顶至底递增，根节点所在层为第 1 层。
节点的度（degree）：节点的子节点数量。在二叉树中，节点的度可以是 0、1 或 2。
二叉树的高度（height）：从根节点到最远叶节点所经过的边的数量。
节点的深度（depth）：从根节点到该节点所经过的边的数量。
节点的高度（height）：从该节点到距离它最远的叶节点所经过的边的数量。

这是图片

2. 二叉树的种类

完全二叉树（Complete Binary Tree）：
- 除了最底层外，每一层的节点数都达到最大，并且最底层的节点都尽可能地靠左对齐。例如，在一个有 3 层的完全二叉树中，第一层和第二层的节点数都达到了最大，第三层的节点从左到右排列，可能不是完全填满的。每个节点的左右子树也都是完全二叉树。
满二叉树（Full Binary Tree）：
- 每个节点要么有两个子节点，要么没有子节点。也就是说，所有的非叶节点都有两个子节点，而所有的叶节点都没有子节点。满二叉树是完全二叉树的一种特殊情况。
平衡二叉树（Balanced Binary Tree）：
- 对于每一个节点，它的左右子树的高度差不超过 1。这种结构可以保证树的操作（如插入、删除、查找）在对数时间复杂度内完成。平衡二叉树的具体实现可以是 AVL 树或红黑树等。
二叉搜索树（Binary Search Tree, BST）：
- 对于每一个节点，左子树的所有节点的值都小于该节点的值，右子树的所有节点的值都大于该节点的值。二叉搜索树用于快速查找、插入和删除操作。
AVL树：
- 一种自平衡的二叉搜索树，任何节点的左右子树的高度差不超过 1。AVL 树通过旋转操作保持树的平衡，从而确保所有基本操作的时间复杂度为 O(log n)。
红黑树（Red-Black Tree）：
- 一种自平衡的二叉搜索树，具有红黑性质来保证树的平衡性。每个节点都有一个颜色（红色或黑色），并且树满足特定的红黑性质，例如从根到任何叶节点的路径上，黑色节点的数量必须相同。这些性质帮助红黑树在插入和删除节点时维持平衡，保证操作的时间复杂度为 O(log n)。

3. 二叉树基本操作

3.1. 初始化二叉树

与链表类似，初始化二叉树需要创建节点并构建它们之间的引用（指针）。

Python 代码示例：

# 定义二叉树节点类
class TreeNode:
    def __init__(self, val, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

# 初始化节点
n1 = TreeNode(val=1)
n2 = TreeNode(val=2)
n3 = TreeNode(val=3)
n4 = TreeNode(val=4)
n5 = TreeNode(val=5)

# 构建节点之间的引用（指针）
n1.left = n2
n1.right = n3
n2.left = n4
n2.right = n5

在这个示例中，我们创建了五个节点，并将它们连接起来，形成了如下结构的二叉树：

3.2. 插入与删除节点

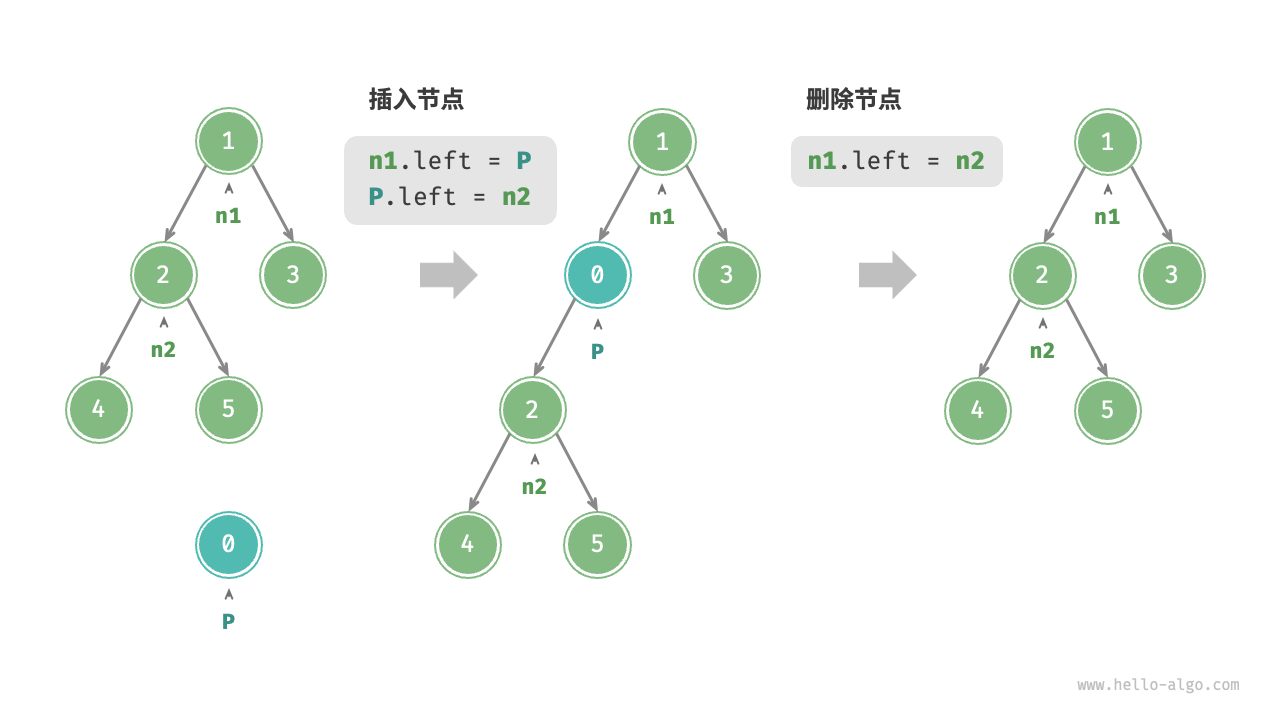
在二叉树中插入和删除节点涉及修改指针以更新树的结构。以下是插入和删除节点的操作示例：

Python 代码示例：

# 定义二叉树节点类（与上面相同）
class TreeNode:
    def __init__(self, val, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

# 创建新节点 p
p = TreeNode(0)

# 在 n1 和 n2 之间插入节点 p
n1.left = p
p.left = n2

# 删除节点 p
n1.left = n2

在这个示例中：

插入操作：我们在节点 n1 的左子节点和 n2 之间插入了一个新节点 p，并将 p 的左子节点设置为 n2。插入后的树结构变为：
```
        1
       / \
      0   3
     / \
    2   5
   /
  4
```
删除操作：为了删除节点 p，我们需要将 n1 的左子节点重新设置为 n2，从而将 p 从树中移除。删除后的树结构恢复为原来的结构：
```
    1
   / \
  2   3
 / \
4   5
```

提示：插入节点可能会改变二叉树的原有结构，而删除节点通常意味着删除该节点及其所有子树。因此，在进行插入和删除操作时，必须确保树的结构符合预期，并维护树的性质（如二叉搜索树的排序性质）。

这是图片

4. 二叉树遍历

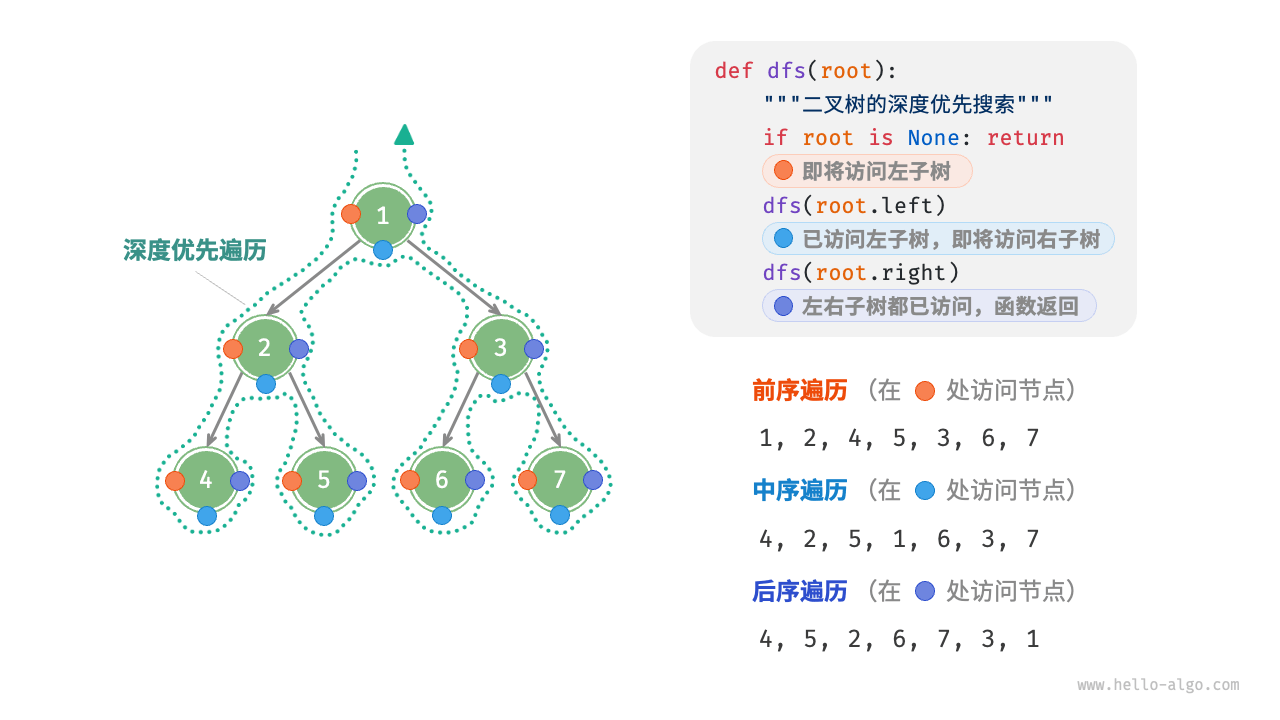
二叉树遍历是对树中的节点进行访问和操作的一种方法。常见的二叉树遍历方式包括前序遍历、中序遍历和后序遍历。每种遍历方式都有其特定的访问顺序。

这是图片

4.1. 前序遍历（Pre-order Traversal）

前序遍历的顺序是：访问根节点 → 遍历左子树 → 遍历右子树。

Python 代码示例：

def pre_order_traversal(root):
    if root is None:
        return
    print(root.val)  # 访问根节点
    pre_order_traversal(root.left)  # 遍历左子树
    pre_order_traversal(root.right)  # 遍历右子树

# 或者

def preorderTraversal(root):
    result = []
    st= []
    if root:
        st.append(root)
    while st:
        node = st.pop()
        if node != None:
            if node.right: #右
                st.append(node.right)
            if node.left: #左
                st.append(node.left)
            st.append(node) #中
            st.append(None)
        else:
            node = st.pop()
            result.append(node.val)
    return result

示例：对于以下二叉树：

前序遍历的结果是：1, 2, 4, 5, 3

4.2. 中序遍历（In-order Traversal）

中序遍历的顺序是：遍历左子树 → 访问根节点 → 遍历右子树。

Python 代码示例：

def in_order_traversal(root):
    if root is None:
        return
    in_order_traversal(root.left)  # 遍历左子树
    print(root.val)  # 访问根节点
    in_order_traversal(root.right)  # 遍历右子树


def inorderTraversal(root):
        result = []
        st = []
        if root:
            st.append(root)
        while st:
            node = st.pop()
            if node != None:
                if node.right: #添加右节点（空节点不入栈）
                    st.append(node.right)
                
                st.append(node) #添加中节点
                st.append(None) #中节点访问过，但是还没有处理，加入空节点做为标记。
                
                if node.left: #添加左节点（空节点不入栈）
                    st.append(node.left)
            else: #只有遇到空节点的时候，才将下一个节点放进结果集
                node = st.pop() #重新取出栈中元素
                result.append(node.val) #加入到结果集
        return result

示例：对于以下二叉树：

中序遍历的结果是：4, 2, 5, 1, 3

4.3. 后序遍历（Post-order Traversal）

后序遍历的顺序是：遍历左子树 → 遍历右子树 → 访问根节点。

Python 代码示例：

def post_order_traversal(root):
    if root is None:
        return
    post_order_traversal(root.left)  # 遍历左子树
    post_order_traversal(root.right)  # 遍历右子树
    print(root.val)  # 访问根节点

def postorderTraversal(root):
        result = []
        st = []
        if root:
            st.append(root)
        while st:
            node = st.pop()
            if node != None:
                st.append(node) #中
                st.append(None)
                
                if node.right: #右
                    st.append(node.right)
                if node.left: #左
                    st.append(node.left)
            else:
                node = st.pop()
                result.append(node.val)
        return result

示例：对于以下二叉树：

后序遍历的结果是：4, 5, 2, 3, 1

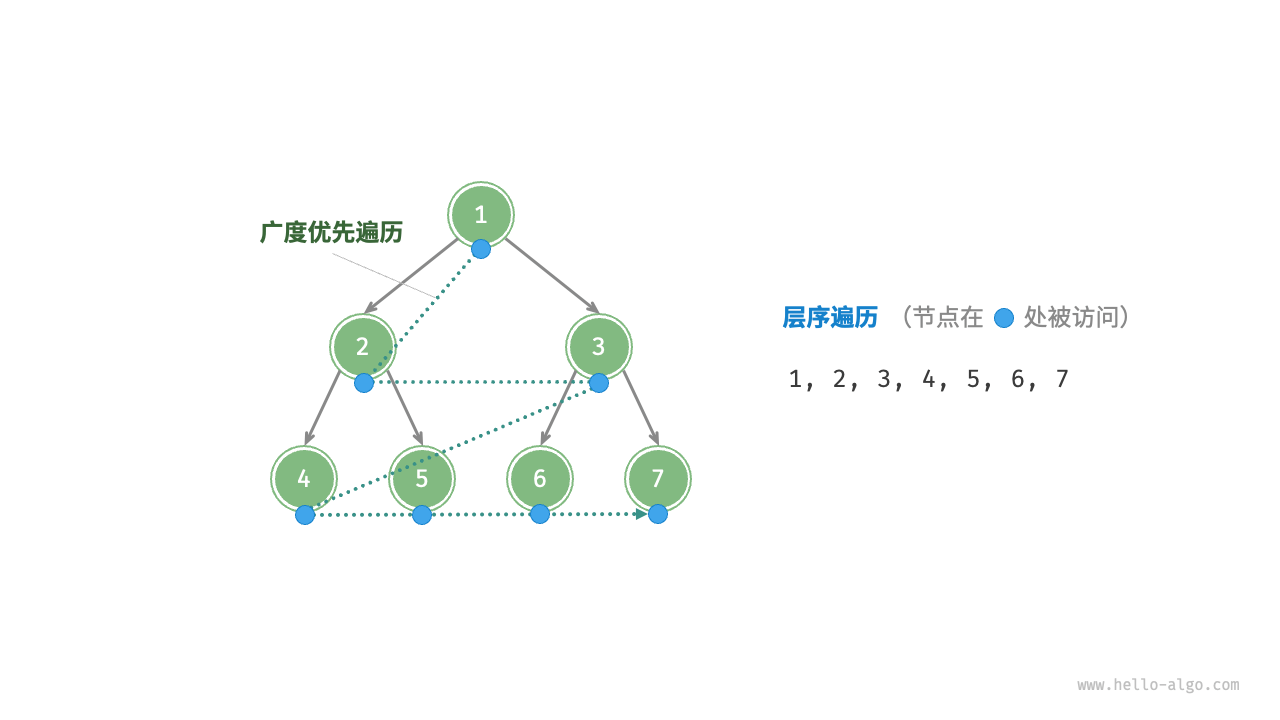
4.4. 层次遍历（Level-order Traversal）

层次遍历也称为广度优先遍历，是按层次从上到下、从左到右遍历节点。通常使用队列来实现。

这是图片

Python 代码示例：

from collections import deque

def level_order_traversal(root):
    if root is None:
        return
    queue = deque([root])
    while queue:
        node = queue.popleft()
        print(node.val)  # 访问节点
        if node.left:
            queue.append(node.left)  # 将左子节点入队
        if node.right:
            queue.append(node.right)  # 将右子节点入队

示例：对于以下二叉树：

层次遍历的结果是：1, 2, 3, 4, 5

5. 二叉树的数组表示

5.1. 完美二叉树的数组表示

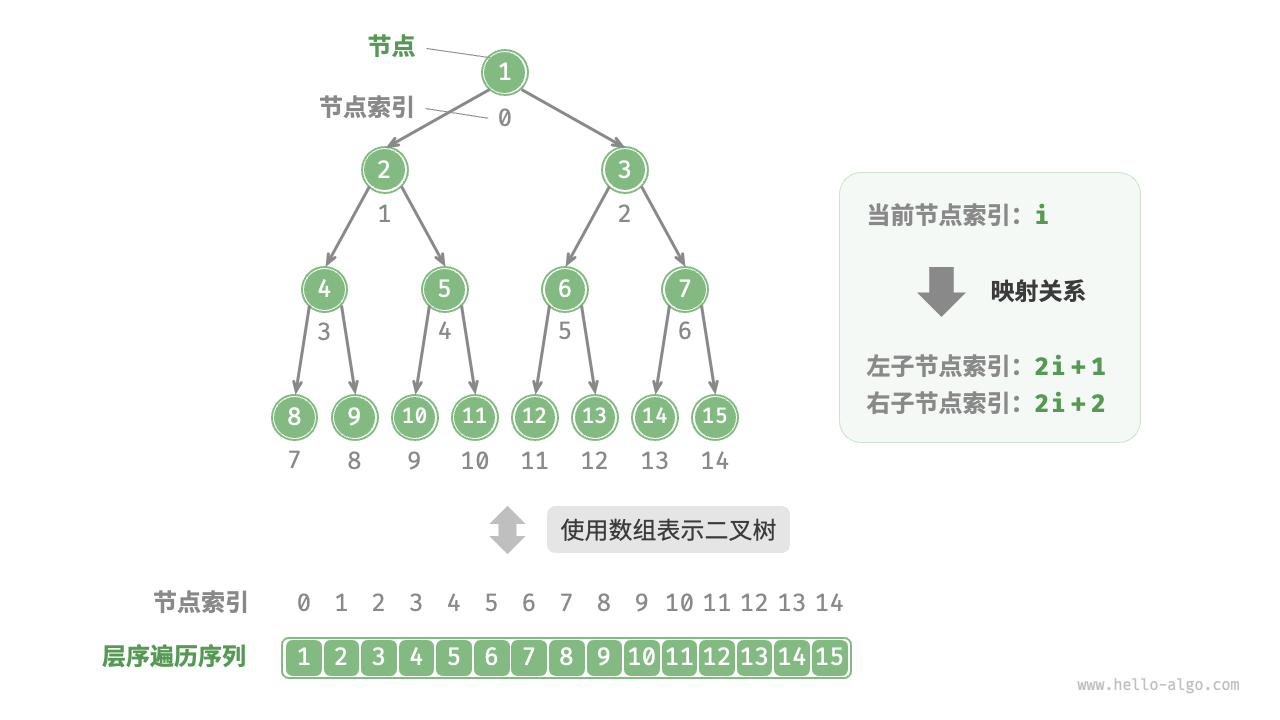
在完美二叉树的数组表示中，映射公式的作用类似于链表中的节点引用（指针）。通过这种方法，我们可以直接访问数组中的任意节点的左子节点或右子节点，而无需显式的指针或引用。

具体来说，假设我们有一棵完美二叉树，并将所有节点按照层序遍历的顺序存储在一个数组中。这样，树中的每个节点都与数组中的一个唯一索引相对应。

根据层序遍历的特性，我们可以推导出父节点与子节点之间的映射公式。假设某个节点在数组中的索引为 ( i )，那么：

该节点的左子节点的索引为 ( 2i + 1 )。
该节点的右子节点的索引为 ( 2i + 2 )。

这些公式使得我们可以高效地从一个节点快速找到其子节点，而不需要额外的存储或复杂的计算。

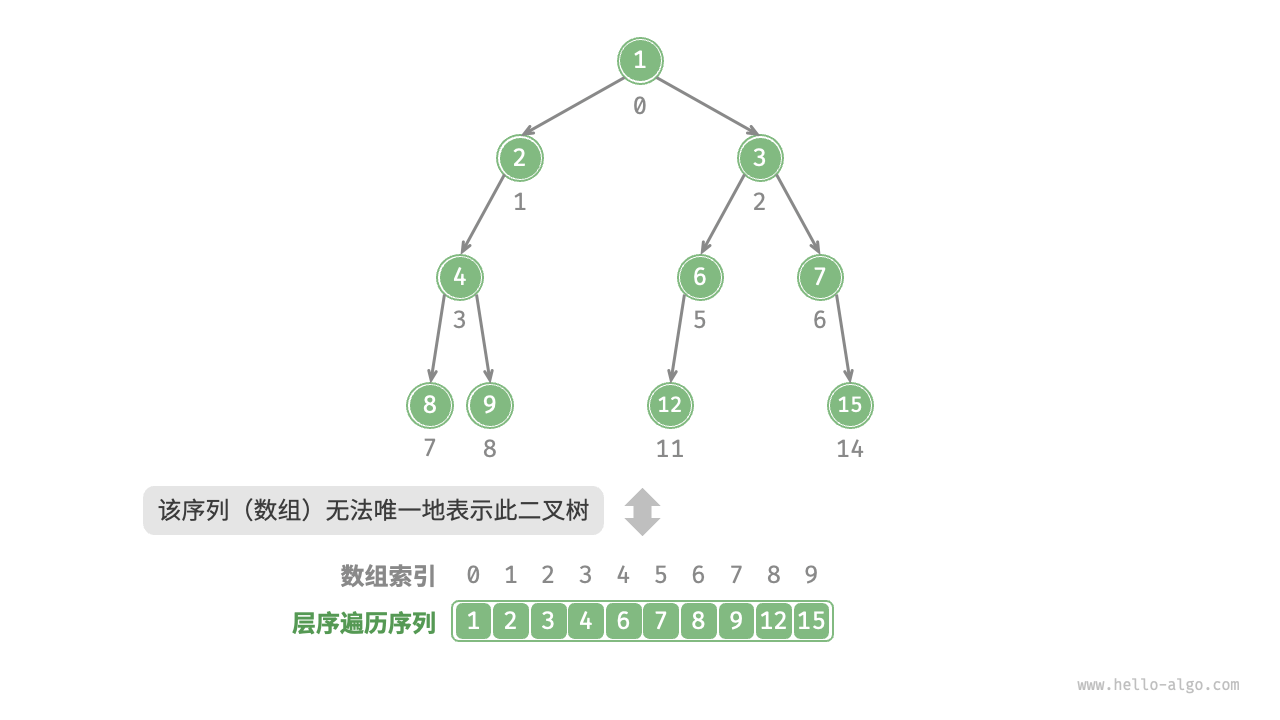
5.2. 非完美二叉树的数组表示

完美二叉树是一个特例，在二叉树的中间层通常会有许多 None（空节点）。由于层序遍历序列并不包含这些 None，我们无法仅凭该序列来推测 None 的数量和分布位置。因此，存在多种二叉树结构都可能符合同一个层序遍历序列。

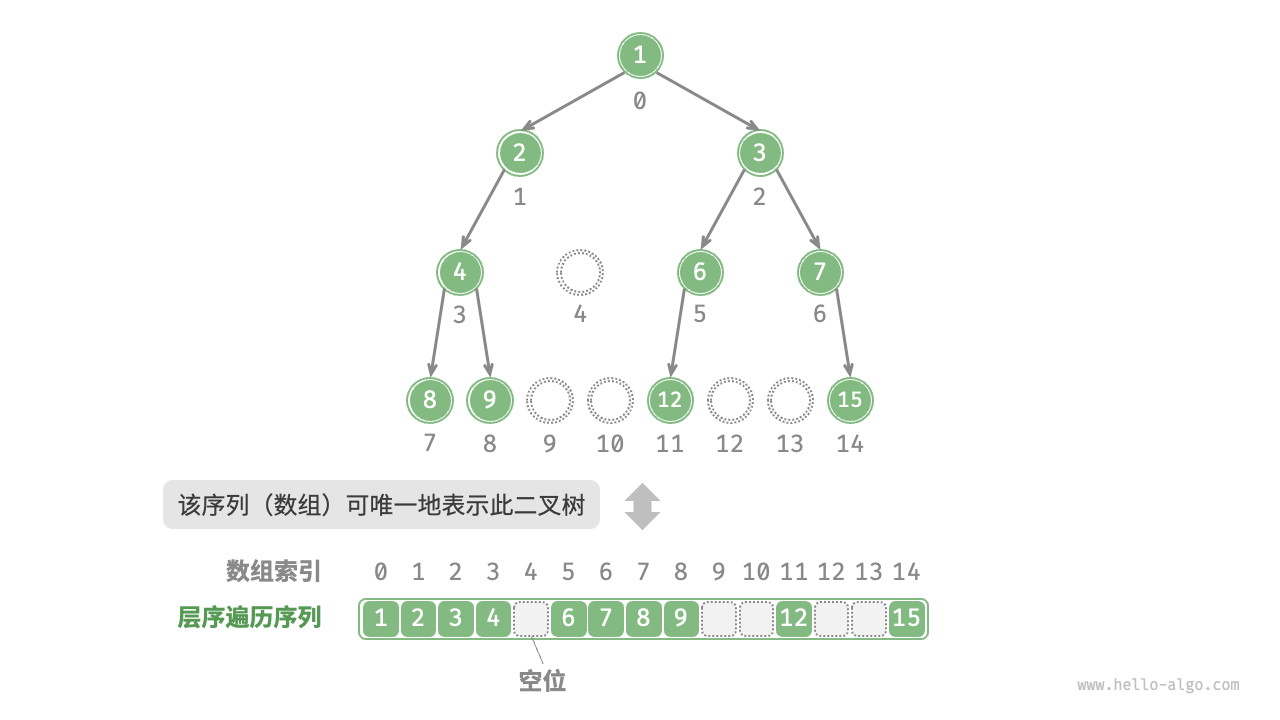
为了解决此问题，我们可以考虑在层序遍历序列中显式地写出所有 None 。

class ArrayBinaryTree:
    def __init__(self, capacity):
        self.tree = [None] * capacity  # Initialize the tree with a fixed capacity
        self.size = 0  # Current number of nodes in the tree

    def add(self, value):
        if self.size >= len(self.tree):
            raise Exception("Tree is full")
        self.tree[self.size] = value
        self.size += 1

    def get_value(self, index):
        if index < 0 or index >= self.size:
            return None
        return self.tree[index]

    def get_left_child(self, index):
        left_index = 2 * index + 1
        if left_index >= self.size:
            return None
        return self.tree[left_index]

    def get_right_child(self, index):
        right_index = 2 * index + 2
        if right_index >= self.size:
            return None
        return self.tree[right_index]

    def get_parent(self, index):
        if index == 0 or index >= self.size:
            return None
        parent_index = (index - 1) // 2
        return self.tree[parent_index]

    def preorder_traversal(self, index=0, result=None):
        if result is None:
            result = []
        if index >= self.size or self.tree[index] is None:
            return result
        result.append(self.tree[index])
        self.preorder_traversal(2 * index + 1, result)
        self.preorder_traversal(2 * index + 2, result)
        return result

    def inorder_traversal(self, index=0, result=None):
        if result is None:
            result = []
        if index >= self.size or self.tree[index] is None:
            return result
        self.inorder_traversal(2 * index + 1, result)
        result.append(self.tree[index])
        self.inorder_traversal(2 * index + 2, result)
        return result

    def postorder_traversal(self, index=0, result=None):
        if result is None:
            result = []
        if index >= self.size or self.tree[index] is None:
            return result
        self.postorder_traversal(2 * index + 1, result)
        self.postorder_traversal(2 * index + 2, result)
        result.append(self.tree[index])
        return result

    def level_order_traversal(self):
        result = []
        for i in range(self.size):
            if self.tree[i] is not None:
                result.append(self.tree[i])
        return result

示例使用：

if __name__ == "__main__":
    tree = ArrayBinaryTree(10)
    nodes = [1, 2, 3, 4, 5, 6, 7]
    for node in nodes:
        tree.add(node)

    print("节点0的值:", tree.get_value(0))
    print("节点1的左子节点:", tree.get_left_child(1))
    print("节点2的右子节点:", tree.get_right_child(2))
    print("节点3的父节点:", tree.get_parent(3))

    print("前序遍历:", tree.preorder_traversal())
    print("中序遍历:", tree.inorder_traversal())
    print("后序遍历:", tree.postorder_traversal())
    print("层序遍历:", tree.level_order_traversal())

输出：

节点0的值: 1
节点1的左子节点: 4
节点2的右子节点: 7
节点3的父节点: 2
前序遍历: [1, 2, 4, 5, 3, 6, 7]
中序遍历: [4, 2, 5, 1, 6, 3, 7]
后序遍历: [4, 5, 2, 6, 7, 3, 1]
层序遍历: [1, 2, 3, 4, 5, 6, 7]

详细说明：

初始化二叉树：
- __init__ 方法创建一个固定容量的数组来表示二叉树，并初始化当前大小为0。
添加节点：
- add 方法在数组中顺序添加节点。如果树已满，则抛出异常。
获取节点值：
- get_value 方法根据给定的索引返回节点的值。如果索引无效，返回 None。
获取左子节点：
- get_left_child 方法计算左子节点的索引 2 * index + 1，并返回对应的值。
获取右子节点：
- get_right_child 方法计算右子节点的索引 2 * index + 2，并返回对应的值。
获取父节点：
- get_parent 方法计算父节点的索引 (index - 1) // 2，并返回对应的值。
遍历方法：
- 前序遍历 (preorder_traversal)： 递归地访问当前节点、左子节点和右子节点。
- 中序遍历 (inorder_traversal)： 递归地访问左子节点、当前节点和右子节点。
- 后序遍历 (postorder_traversal)： 递归地访问左子节点、右子节点和当前节点。
- 层序遍历 (level_order_traversal)： 按照节点在数组中的顺序依次访问。

注意事项：

该实现假设二叉树是完全二叉树或接近完全的二叉树，以充分利用数组结构。
如果需要动态扩展树的容量，可以在 add 方法中添加自动扩容的逻辑。
为了简化实现，未处理删除节点的操作。如果需要删除功能，需要额外的逻辑处理。

5.3. 优点与局限性

二叉树的数组表示具有以下优点：

缓存友好：数组存储在连续的内存空间中，这使得对缓存的利用更加高效，进而提高访问和遍历的速度。
节省空间：不需要额外存储指针，因此比链式结构节省空间。
允许随机访问：可以通过索引直接访问任意节点，提供了高效的随机访问能力。

然而，数组表示也存在一些局限性：

内存连续性要求：数组需要连续的内存空间，这对于存储数据量较大的树可能不适用。
增删节点的低效：在树的插入和删除操作中，数组需要进行元素的移动和重新排列，这些操作的效率较低。
空间利用率低：当树中包含大量 None（空）节点时，数组中的有效节点数据比重较低，导致空间利用率降低。

6. 二叉搜索树(BST)

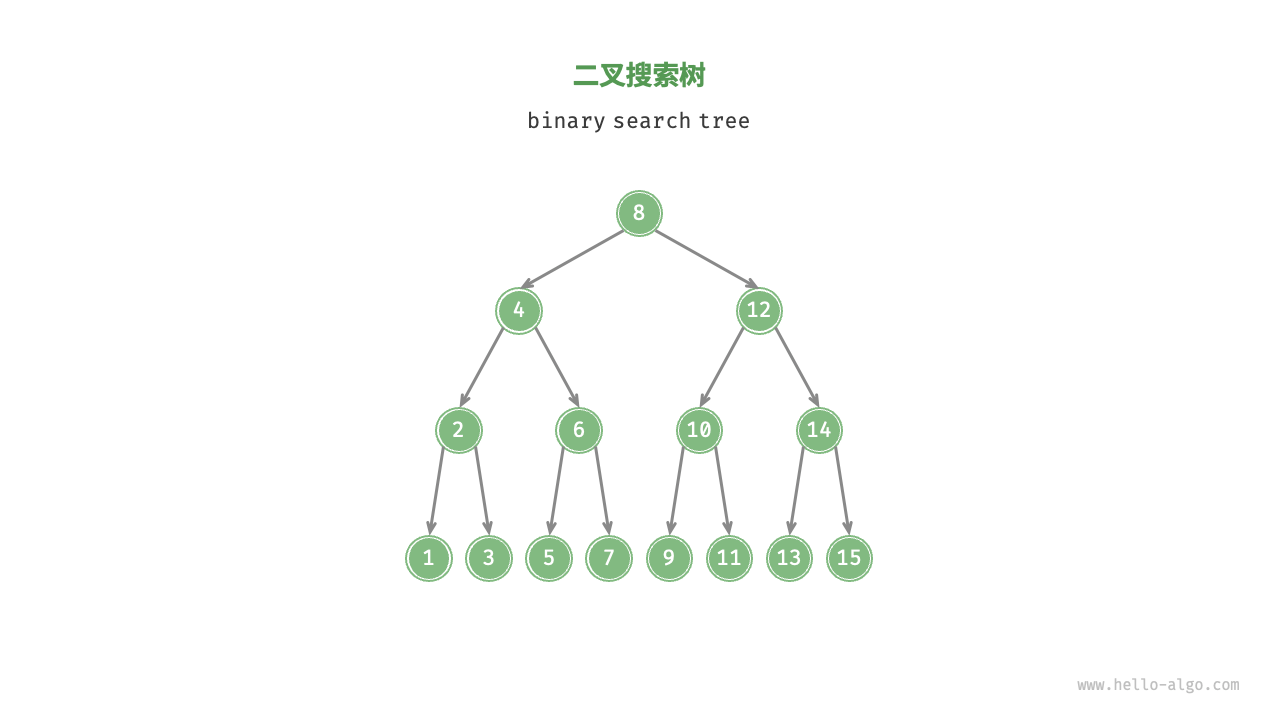
二叉搜索树（Binary Search Tree, BST）满足以下条件：

对于任意一个节点，其左子树中所有节点的值都小于该节点的值，而右子树中所有节点的值都大于该节点的值。
任意节点的左、右子树也都是二叉搜索树，因此同样满足上述条件。

6.1 二叉搜索树的操作

我们将二叉搜索树封装为一个类 BinarySearchTree，并声明一个成员变量 root，用于指向树的根节点。

6.1.1 查找节点

给定目标节点值 num，可以利用二叉搜索树的性质进行查找。如下图所示，我们声明一个节点 cur，从二叉树的根节点 root 出发，逐步比较节点值 cur.val 和 num 之间的大小关系：

如果 cur.val < num，说明目标节点在 cur 的右子树中，因此执行 cur = cur.right。
如果 cur.val > num，说明目标节点在 cur 的左子树中，因此执行 cur = cur.left。
如果 cur.val = num，说明找到了目标节点，跳出循环并返回该节点。

二叉搜索树的查找操作与二分查找算法类似，都是通过每次排除一半的可能性来缩小搜索范围。查找的循环次数最多为二叉树的高度，因此在平衡的二叉搜索树中，查找操作的时间复杂度为 $O(\log n)$。示例代码如下：

6.1.2 插入节点

给定一个待插入的元素 num，为了保持二叉搜索树“左子树 < 根节点 < 右子树”的性质，插入操作的流程如下：

查找插入位置：与查找操作相似，从根节点出发，根据当前节点值与 num 的大小关系逐层向下搜索，直到越过叶节点（即遍历至 None）时跳出循环。
在该位置插入节点：初始化节点 num，并将该节点插入到 None 的位置。

在代码实现中需要注意以下两点：

二叉搜索树不允许存在重复的节点，否则会违反其定义。因此，如果待插入的节点在树中已存在，则不执行插入操作，直接返回。
为了实现插入操作，我们需要借助节点 pre 来保存上一轮循环中的节点位置。这样在遍历至 None 时，我们可以通过 pre 获取到其父节点，从而完成插入操作。

插入节点的时间复杂度与查找操作相同，也是 $O(\log n)$。

6.1.3 删除节点

删除节点的操作首先要在二叉树中找到目标节点，然后将其删除。与插入节点类似，删除操作需要保证二叉搜索树的“左子树 < 根节点 < 右子树”的性质在操作完成后仍然成立。根据目标节点的子节点数量，删除操作可以分为以下三种情况：

节点没有子节点：直接删除该节点。
节点有一个子节点：删除该节点，并用其唯一的子节点替代它。
节点有两个子节点：在这种情况下，不能直接删除该节点，需要用一个节点替代它。这个替代节点可以是右子树的最小节点（即中序遍历的后继节点）或左子树的最大节点。

假设选择右子树的最小节点（中序遍历的后继节点）进行替换，删除操作的流程如下：

找到待删除节点在“中序遍历序列”中的下一个节点，记为 tmp。
用 tmp 的值替换待删除节点的值，并在树中递归删除节点 tmp。

删除节点操作的时间复杂度为 $O(\log n)$，其中查找待删除节点和获取中序遍历后继节点均需 $O(\log n)$ 时间。

下面是 BinarySearchTree 类的实现，其中包括查找、插入和删除节点的操作：

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class BinarySearchTree:
    def __init__(self):
        self.root = None

    def search(self, num: int) -> TreeNode:
        cur = self.root
        while cur:
            if cur.val == num:
                return cur
            elif cur.val < num:
                cur = cur.right
            else:
                cur = cur.left
        return None

    def insert(self, num: int) -> None:
        if not self.root:
            self.root = TreeNode(num)
            return

        cur = self.root
        pre = None
        while cur:
            pre = cur
            if cur.val == num:
                return  # 不插入重复的节点
            elif cur.val < num:
                cur = cur.right
            else:
                cur = cur.left

        # 插入新节点
        if pre.val < num:
            pre.right = TreeNode(num)
        else:
            pre.left = TreeNode(num)

    def delete(self, num: int) -> None:
        self.root = self._delete_node(self.root, num)

    def _delete_node(self, root: TreeNode, num: int) -> TreeNode:
        if not root:
            return None

        if num < root.val:
            root.left = self._delete_node(root.left, num)
        elif num > root.val:
            root.right = self._delete_node(root.right, num)
        else:
            # 找到待删除节点
            if not root.left:  # 没有左子树，直接返回右子树
                return root.right
            elif not root.right:  # 没有右子树，直接返回左子树
                return root.left
            
            # 有两个子节点，寻找右子树的最小节点
            min_larger_node = self._find_min(root.right)
            root.val = min_larger_node.val  # 用右子树的最小节点替换
            root.right = self._delete_node(root.right, min_larger_node.val)  # 删除右子树中的最小节点
        
        return root

    def _find_min(self, root: TreeNode) -> TreeNode:
        while root.left:
            root = root.left
        return root

代码解析

查找节点 (search):
- 从根节点开始，根据 num 和当前节点值的比较结果，决定向左还是向右子树移动。
- 如果找到了节点，则返回该节点；如果遍历到叶节点仍未找到，则返回 None。
插入节点 (insert):
- 从根节点开始，找到合适的插入位置后，将新节点插入。
- 若树为空，直接将新节点作为根节点。
- 若要插入的节点值已存在于树中，则不进行插入操作。
删除节点 (delete):
- 首先找到要删除的节点，然后根据该节点的子节点情况进行不同的删除操作：
  - 如果没有子节点，直接删除该节点。
  - 如果只有一个子节点，用该子节点替换删除的节点。
  - 如果有两个子节点，用右子树的最小节点（或左子树的最大节点）替换删除的节点，然后递归删除该最小节点。

这些操作均在 O(\log n) 时间复杂度下完成，其中 n 为二叉树的节点个数，适用于平衡的二叉搜索树。

6.1.5 中序遍历有序

如图所示，二叉树的中序遍历遵循“左子树 -> 根节点 -> 右子树”的顺序，而二叉搜索树满足“左子节点 < 根节点 < 右子节点”的大小关系。

这意味着，在二叉搜索树中进行中序遍历时，总是会按从小到大的顺序访问节点。因此，二叉搜索树的中序遍历结果是一个有序的序列。

利用二叉搜索树的这一性质，我们可以在 $O(n)$ 时间内获取有序的数据，无需额外的排序操作，非常高效。

6.2 二叉搜索树的效率

在面对一组数据时，可以选择使用数组或二叉搜索树进行存储。如下表所示，二叉搜索树的各项操作的时间复杂度通常为对数阶，因此具有较高的性能。只有在高频添加、低频查找删除的场景中，数组的效率才会优于二叉搜索树。

表 1: 数组与二叉搜索树的效率对比

	无序数组	二叉搜索树
查找元素	$O(n)$	$O(\log n)$
插入元素	$O(1)$	$O(\log n)$
删除元素	$O(n)$	$O(\log n)$

在理想情况下，二叉搜索树是“平衡”的，因此可以在 $\log n$ 次操作内查找任意节点。

然而，如果在二叉搜索树中反复插入和删除节点，树可能会退化为链表，这时各种操作的时间复杂度将会降至 $O(n)$。

6.3 二叉搜索树的常见应用

用作系统中的多级索引，实现高效的查找、插入和删除操作。
作为某些搜索算法的底层数据结构。
用于存储数据流，以保持其有序状态。

算法与数据结构 (Algorithms and Data Structures)

二叉树(8)

1. 基本概念

2. 二叉树的种类

3. 二叉树基本操作

3.1. 初始化二叉树

3.2. 插入与删除节点

4. 二叉树遍历

4.1. 前序遍历（Pre-order Traversal）

4.2. 中序遍历（In-order Traversal）

4.3. 后序遍历（Post-order Traversal）

4.4. 层次遍历（Level-order Traversal）

5. 二叉树的数组表示

5.1. 完美二叉树的数组表示

5.2. 非完美二叉树的数组表示

5.3. 优点与局限性

6. 二叉搜索树(BST)

6.1 二叉搜索树的操作

6.1.1 查找节点

6.1.2 插入节点

6.1.3 删除节点

代码解析

6.1.5 中序遍历有序

6.2 二叉搜索树的效率

6.3 二叉搜索树的常见应用

CATALOG

FEATURED TAGS

FRIENDS