Data Structure

算法与数据结构 (Algorithms and Data Structures)

链表(4)

Posted by 月月鸟 on September 15, 2021

链表（Linked List）是一种线性数据结构，由一组节点（Node）组成，每个节点包含数据域和指向下一个节点的指针（或引用）。链表具有灵活的内存分配方式，适用于需要频繁插入和删除操作的场景。

1. 链表的结构

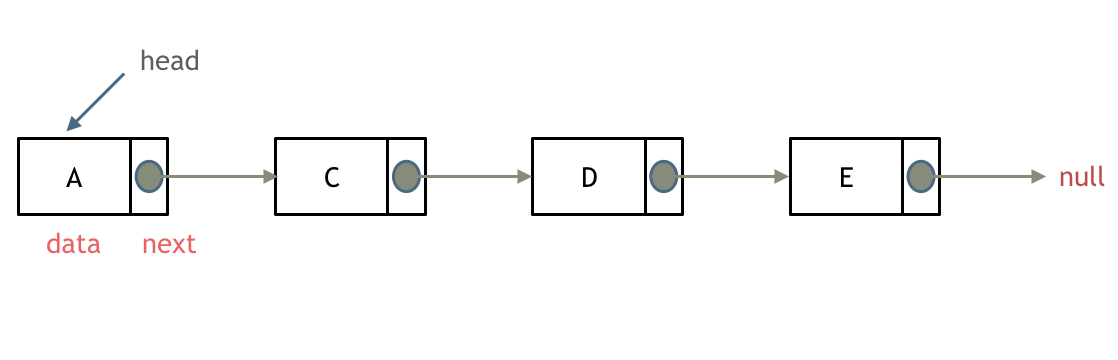
每个节点通常包含两个部分：

  1. 数据域（Data）： 用于存储数据，可以是任何数据类型。
  2. 指针域（Next）： 存储指向下一个节点的指针（或引用）。

链表通过每个节点中的指针域连接在一起，从而形成一个链状结构。

1

2. 链表的类型

  1. 单向链表（Singly Linked List）：
    • 每个节点只有一个指向下一个节点的指针。
    • 只能从头到尾顺序访问。
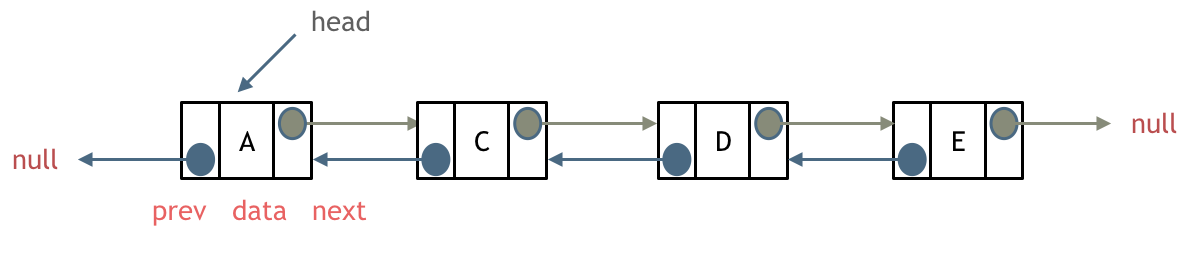
  2. 双向链表（Doubly Linked List）：
    • 每个节点有两个指针，分别指向前一个节点和后一个节点。
    • 可以双向遍历，访问更加灵活。 1
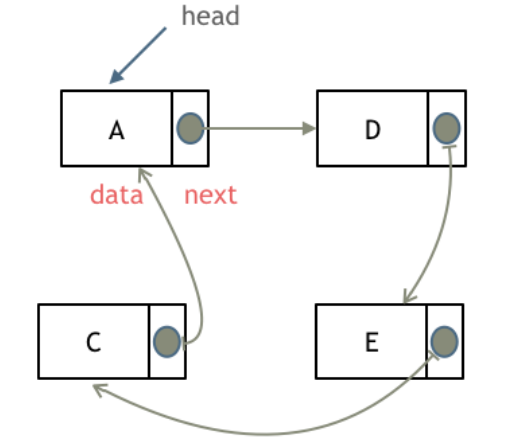
  3. 循环链表（Circular Linked List）：
    • 最后一个节点的指针指向第一个节点，形成一个环。
    • 可以是单向循环或双向循环链表。 1

3. 链表的存储方式

链表在内存中的存储方式与数组不同。与数组的连续内存分布相比，链表中的节点在内存中是分散的。链表通过每个节点中的指针域链接不同的节点，这些节点的内存地址并不连续，而是由操作系统的内存管理机制动态分配。每个节点包含的数据部分和指针部分，其中指针部分负责指向下一个（或前一个）节点，实现链表的结构。这样的存储方式使得链表在动态插入和删除操作时更加灵活，但也使得内存的分布更加分散。

4. 链表的优缺点

优点：

  • 动态大小： 链表不需要预先分配固定大小的内存，可以根据需要动态增长。
  • 快速插入和删除： 在已知节点位置的情况下，插入和删除操作仅需修改指针，不需要移动其他元素。

缺点：

  • 内存开销大： 每个节点需要额外的指针域，占用更多内存。
  • 访问速度慢： 访问链表中的第n个元素需要从头遍历，平均时间复杂度为O(n)。

5. 链表的基本操作

5.1 链表节点类

class Node:
    def __init__(self, value):
        self.value = value  # 节点的值
        self.next = None    # 指向下一个节点的指针

5.2 链表的初始化

建立链表分为两步，第一步是初始化各个节点对象，第二步是构建节点之间的引用关系。初始化完成后，我们就可以从链表的头节点出发，通过引用指向next依次访问所有节点。

# 初始化链表 1 -> 3 -> 2 -> 5 -> 4
# 初始化各个节点
n0 = ListNode(1)
n1 = ListNode(3)
n2 = ListNode(2)
n3 = ListNode(5)
n4 = ListNode(4)
# 构建节点之间的引用
n0.next = n1
n1.next = n2
n2.next = n3
n3.next = n4

5.3 插入节点

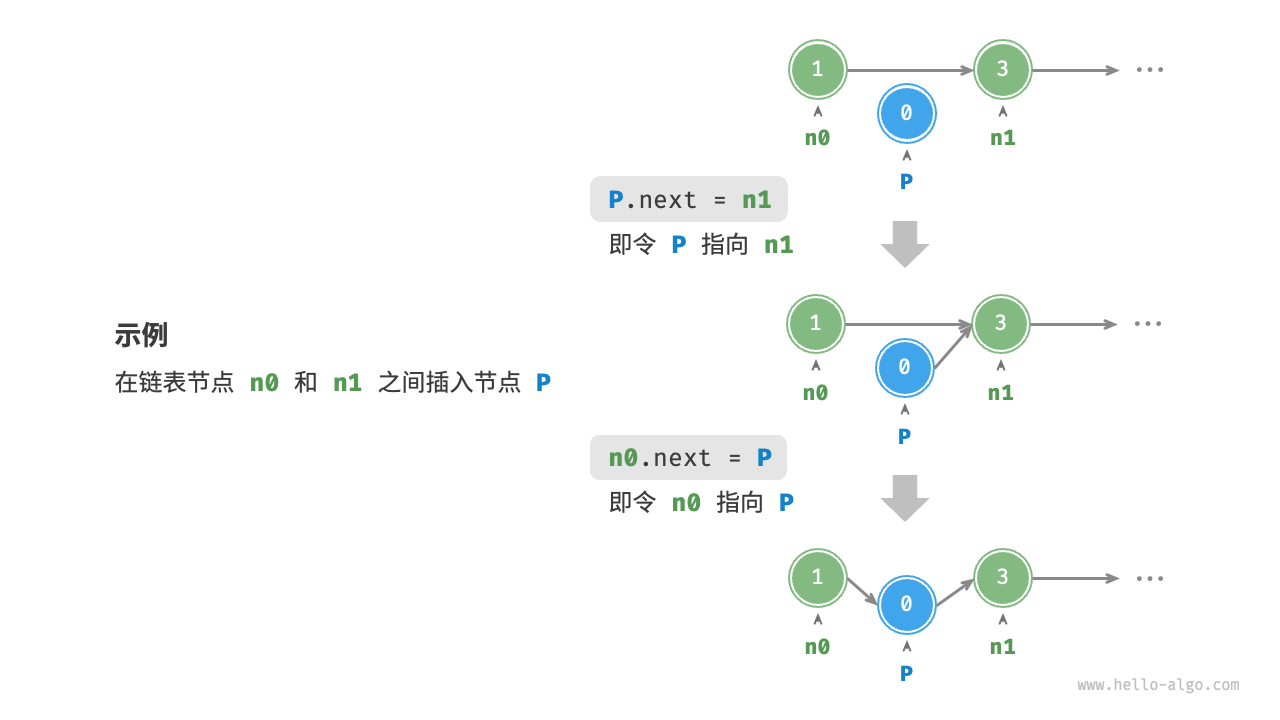
在链表中插入节点非常简单。例如，如图所示，假设我们希望在两个相邻节点 n0 和 n1 之间插入一个新节点 P，只需调整 n0 的 next 指针和 P 的 next 指针即可。这一操作的时间复杂度为 ( O(1) )。

相比之下，在数组中插入元素的时间复杂度为 ( O(n) )，因为在插入位置之后的所有元素需要向后移动一个位置，这在大数据量的情况下效率较低。

1

    def append(self, value):
        """在链表末尾插入节点"""
        new_node = Node(value)
        if self.head is None:
            self.head = new_node
        else:
            current = self.head
            while current.next:
                current = current.next
            current.next = new_node

    def insert_at_beginning(self, value):
        """在链表开头插入节点"""
        new_node = Node(value)
        new_node.next = self.head
        self.head = new_node

    def insert_after(self, prev_value, value):
        """在指定节点之后插入新节点"""
        current = self.head
        while current and current.value != prev_value:
            current = current.next
        if current is None:
            print(f"Node with value {prev_value} not found.")
            return
        new_node = Node(value)
        new_node.next = current.next
        current.next = new_node

5.4 删除节点

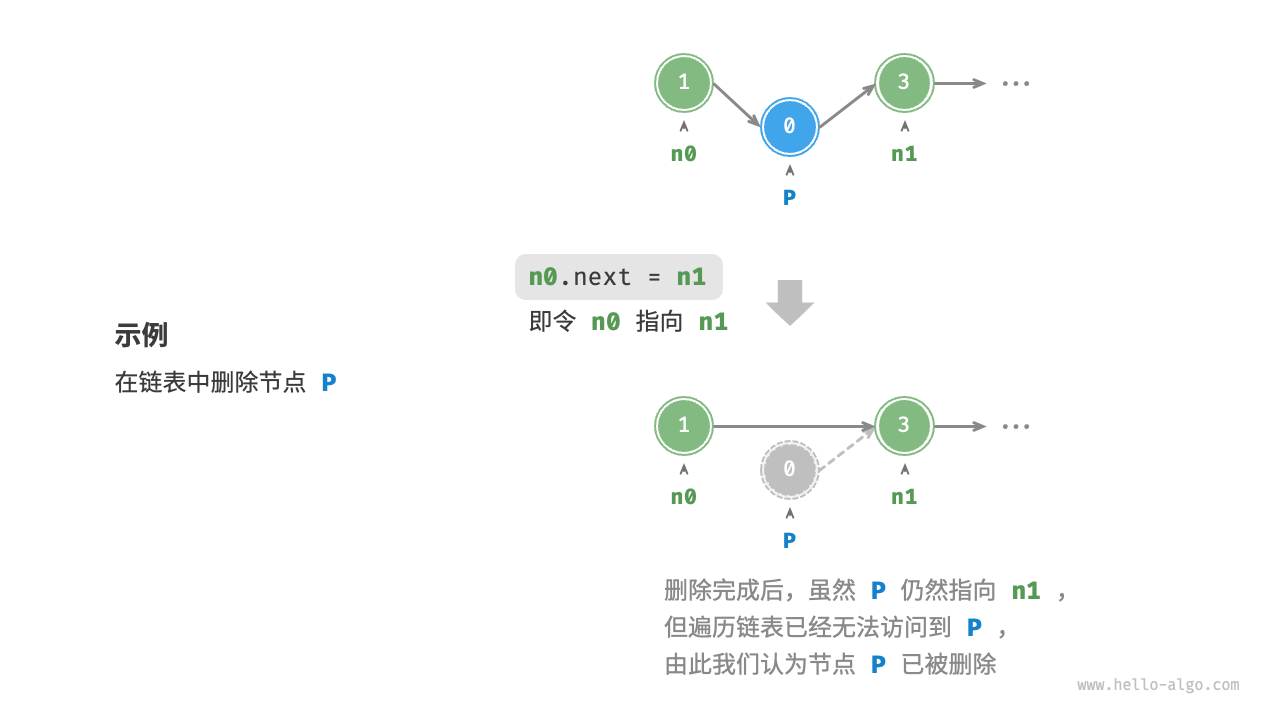
在链表中删除节点也非常方便，只需改变一个节点的引用（指针）即可。请注意，尽管在删除操作完成后节点 P 仍然指向 n1 ，但实际上遍历此链表已经无法访问到 P ，这意味着 P 已经不再属于该链表了。

1

def delete_head(self):
        """删除链表的头节点"""
        if self.head is not None:
            self.head = self.head.next

def delete_tail(self):
    """删除链表的尾节点"""
    if self.head is None:
        print("The list is empty.")
        return
    if self.head.next is None:
        self.head = None
        return
    current = self.head
    while current.next and current.next.next:
        current = current.next
    current.next = None

def delete_value(self, value):
    """删除链表中第一个匹配指定值的节点"""
    current = self.head
    previous = None
    while current and current.value != value:
        previous = current
        current = current.next
    if current is None:
        print(f"Value {value} not found in the list.")
        return
    if previous is None:
        self.head = current.next
    else:
        previous.next = current.next

5.5 访问节点

在链表中访问节点的效率较低。与数组不同，我们可以在 ( O(1) ) 时间内直接访问数组中的任意元素。对于链表，程序需要从头节点开始，逐个向后遍历，直到找到目标节点。这意味着，访问链表中的第 ( n ) 个节点需要循环 ( n-1 ) 轮，时间复杂度为 ( O(n) )。

def get_node_at_index(self, index):
        """获取链表中第 index 个节点的值"""
        current = self.head
        count = 0
        while current:
            if count == index:
                return current.value
            current = current.next
            count += 1
        raise IndexError("Index out of bounds")

    def display(self):
        """显示链表中的所有节点"""
        current = self.head
        while current:
            print(current.value, end=" -> ")
            current = current.next
        print("None")

5.6 查找节点

遍历链表，查找其中值为 target 的节点，输出该节点在链表中的索引。此过程也属于线性查找。

def find_node(self, value):
        """查找链表中第一个匹配指定值的节点"""
        current = self.head
        while current:
            if current.value == value:
                return current  # 返回找到的节点
            current = current.next
        return None  # 如果没有找到节点，返回 None

6. 数组 vs. 链表

该表总结了数组和链表的各项特点并对比了操作效率。由于它们采用两种相反的存储策略，因此各种性质和操作效率也呈现对立的特点。

特性 数组 链表
存储方式 连续内存空间 分散内存空间
容量扩展 长度不可变 可灵活扩展
内存效率 元素占用内存少，但可能浪费空间 元素占用内存多
访问元素 ( O(1) ) ( O(n) )
添加元素 ( O(n) ) ( O(1) )
删除元素 ( O(n) ) ( O(1) )

7. 链表典型应用¶

在数据结构和算法的学习中，单向链表和双向链表扮演着至关重要的角色。它们不仅基础且灵活，可以实现多种高级数据结构和解决多样的编程问题。 单向链表的典型应用包括：

  1. 栈与队列：
    • 栈（Stack）：实现为只在一端进行插入和删除操作的单向链表，遵循先进后出（LIFO）的原则。
    • 队列（Queue）：插入操作在链表的一端进行，而删除操作在另一端进行，符合先进先出（FIFO）的原则。
  2. 哈希表：
    • 用来解决哈希冲突，链表中可以存放哈希相同的多个元素，这种方法称为链式地址法。
  3. 图的表示：
    • 通过邻接表来表示，每个顶点通过一个链表与其相邻的顶点相连。

双向链表，具有指向前一个和后一个节点的链接，使得它在以下场景中特别有用：

  1. 高级数据结构：
    • 如红黑树和B树，节点中含有指向父节点的引用，便于遍历和管理。
  2. 浏览器历史记录：
    • 双向链表可以方便地实现前进和后退功能，通过简单地移动到前一个或后一个节点。
  3. LRU缓存淘汰算法：
    • 双向链表支持高效的节点添加和删除操作，适合实现最近最少使用（LRU）的缓存策略。

环形链表特别适用于周期性操作，如：

  1. 时间片轮转调度算法：
    • 在操作系统中，环形链表可以用来循环安排进程的执行，确保每个进程公平地获得CPU时间。
  2. 数据缓冲区：
    • 在多媒体应用中，环形链表帮助实现音视频数据的连续播放，通过循环利用缓冲区块。

8. 链表力扣题

8.1 移除链表元素

  1. 初始化: dummy_head 节点被初始化为一个值为 0 的新节点，并且其 next 指针指向原链表的头节点。这样，如果原链表的头节点需要被删除，虚拟头节点 dummy_head 可以帮助我们轻松处理这种情况。

  2. 遍历链表: 在 while 循环中，current 指针从 dummy_head 开始，遍历链表并检查 current.next 节点的值。如果 current.next.val 等于要删除的值 val，则跳过该节点（即 current.next = current.next.next），否则就移动到下一个节点（即 current = current.next）。

  3. 返回结果: 遍历完成后，dummy_head.next 是删除指定值后的链表的新头节点。如果我们返回 current，我们可能会丢失链表的起始部分，因为 current 指向的是删除操作之后的最后一个节点。

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next

class Solution:
    def removeElements(self, head: Optional[ListNode], val: int) -> Optional[ListNode]:

        dummy_head = ListNode(0, next = head)
        current = dummy_head
        
        while current.next:
            if current.next.val == val:
                current.next = current.next.next
            else:
                current = current.next
        
        return dummy_head.next

8.2 设计链表


class ListNode:
    def __init__(self, val=0, next=None):
        self.val = val
        self.next = next

class MyLinkedList:

    def __init__(self):
        self.dummy_head = ListNode()
        self.size = 0

    def get(self, index: int) -> int:
        if index < 0 or index >= self.size:
            return -1

        current = self.dummy_head.next
        for _ in range(index):
            current = current.next
        return current.val

    def addAtHead(self, val: int) -> None:
        new_node = ListNode(val, self.dummy_head.next)
        self.dummy_head.next = new_node
        self.size += 1

    def addAtTail(self, val: int) -> None:
        current = self.dummy_head
        while current.next:
            current = current.next
        current.next = ListNode(val)
        self.size += 1

    def addAtIndex(self, index: int, val: int) -> None:
        if index < 0 or index > self.size:
            return

        new_node = ListNode(val)
        current = self.dummy_head
        for _ in range(index):
            current = current.next
        new_node.next = current.next
        current.next = new_node
        self.size += 1

    def deleteAtIndex(self, index: int) -> None:
        if index < 0 or index >= self.size:
            return

        current = self.dummy_head
        for _ in range(index):
            current = current.next
        current.next = current.next.next
        self.size -= 1

8.3 反转链表

首先，定义一个 cur 指针指向头结点，另一个 pre 指针初始化为 null。接下来，我们开始进行链表的反转操作。

  1. 保存当前节点的下一个节点：为了避免在修改指针时丢失当前节点的下一个节点，我们使用一个 tmp 指针保存 cur->next。

  2. 反转当前节点的指针：将 cur->next 指向 pre。此时，当前节点的指向已经完成反转。

  3. 移动指针：将 pre 移动到当前节点的位置（即 pre = cur），将 cur 移动到 tmp 指向的位置（即 cur = tmp），以便继续反转下一个节点。

  4. 重复上述步骤：继续循环，直到 cur 指向 null，此时链表已完成反转。

  5. 返回新的头结点：循环结束后，pre 指针将指向新的头结点。最终，返回 pre。 1

class Solution:
    def reverseList(self, head: Optional[ListNode]) -> Optional[ListNode]:

        cur = head   
        pre = None
        while cur:
            # 保存一下 cur的下一个节点，因为接下来要改变cur->next
            temp = cur.next 
            #反转
            cur.next = pre
            #更新pre、cur指针
            pre = cur
            cur = temp
        return pre

8.4 反转链表

CATALOG
    FEATURED TAGS
    Algorithm Data Structure Machine Learning Deep Learning NLP Computer Vision
    FRIENDS