1. 数组理论基础

1.1 数组的定义

数组作为一种基础的数据结构，在计算机科学领域具有重要的地位，尤其在面试中常常被用来考察候选人的基本编程能力和代码掌控能力。数组问题的核心在于其思维过程通常相对简单，但要将这种思维过程准确地转化为代码实现，往往需要对数组的底层原理和内存管理有深刻的理解。

从内存存储的角度来看，数组是一组相同类型的数据元素的集合，这些数据被紧密地存储在连续的内存地址中。这种连续存储的方式使得数组在访问特定元素时非常高效，因为通过数组的下标索引，可以直接计算出该元素在内存中的位置，从而实现快速访问。这一特性使得数组在需要频繁访问或修改特定位置的数据时表现尤为优越。举一个字符数组的例子，如图所示：

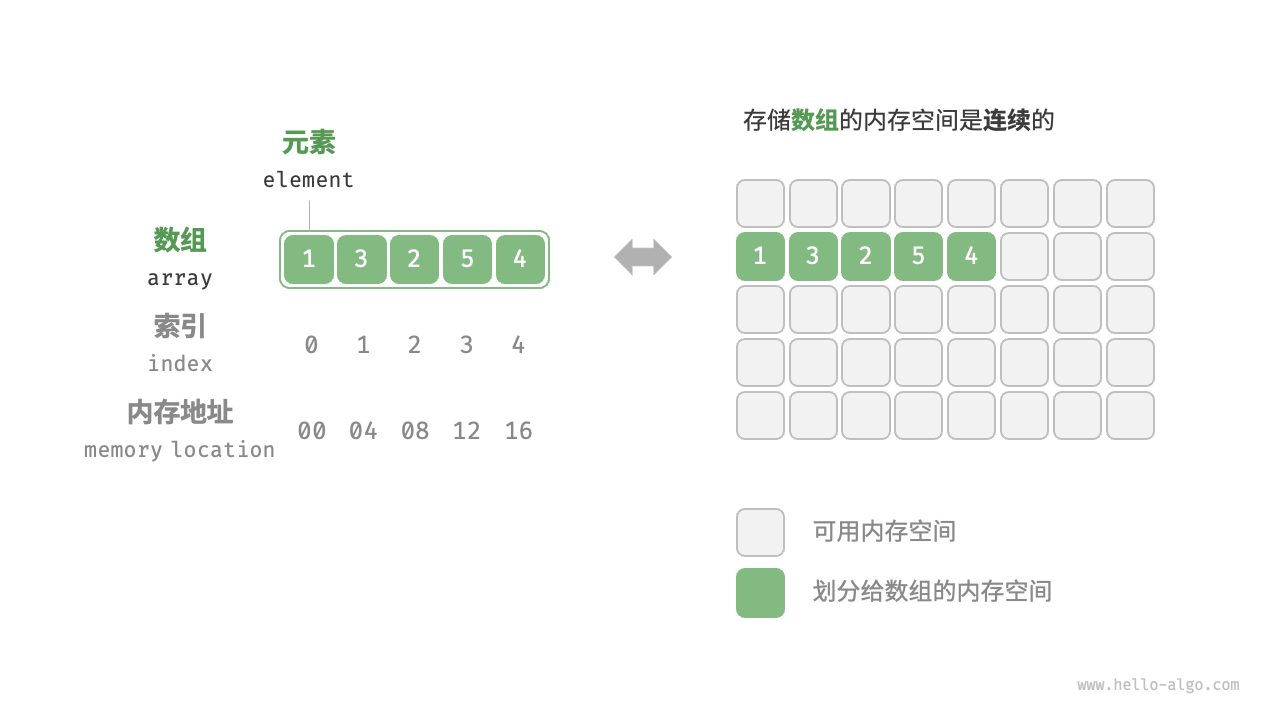
然而，正是由于数组要求数据元素在内存中是连续存储的，因此在数组的初始化和扩展时，需要考虑内存的分配问题。比如，当数组需要扩容时，往往需要在内存中找到一块足够大的连续空间来重新存储数组，这可能会影响程序的性能。

此外，数组的固定大小也是其一个重要特征。一旦数组被创建，其大小通常是固定的，在大多数编程语言中，数组的大小在初始化时就必须确定。虽然这一特性使得数组在使用时更加高效和简单，但在处理动态数据时可能会带来一些限制，需要使用更为灵活的数据结构，如动态数组或链表来解决这些问题。

综上所述，数组作为一种存储相同类型数据的连续集合，具有高效的索引访问和内存利用特点，但在实际使用中，开发者需要对其内存管理特性有清晰的理解，以在代码实现过程中有效地应对数组的局限性。

1.2 数组要注意的地方

数组作为一种基础的数据结构，虽然简单，但其在使用过程中有一些特殊之处和需要注意的事项，尤其在性能和内存管理方，通过理解这些特殊之处，开发者在使用数组时可以更好地预防潜在问题，提高代码的可靠性和性能：

边界条件：在操作数组时，最常见的问题之一是数组越界错误。这种错误发生在尝试访问数组中不存在的索引位置时。例如，在一个长度为 n 的数组中，有效索引是从 0 到 n-1，访问超出这个范围的索引将导致程序错误。因此，编写数组操作代码时，必须特别注意边界条件的处理。
内存消耗：由于数组在内存中占用的是连续的存储空间，这就要求在数组初始化时为其分配足够的内存。如果数组非常大，可能会导致内存不足的问题。此外，数组的大小在初始化时是固定的，如果需要处理动态大小的数据，这可能会导致内存浪费或者不够用的问题。
插入和删除操作的效率：在数组中进行插入和删除操作的效率相对较低，尤其是在数组的中间位置插入或删除元素时。由于数组的连续存储特性，插入或删除一个元素通常需要移动其他元素来保持连续性，这会导致 O(n) 的时间复杂度。对于频繁插入或删除操作的场景，链表可能是更合适的数据结构。
多维数组：在实际应用中，可能会遇到多维数组，如矩阵或更高维度的数据。这些数组的内存布局和访问方式与一维数组略有不同，特别是在内存的行优先或列优先存储方式上。对于性能敏感的应用，理解并利用内存局部性优化多维数组的访问模式是非常重要的。
缓存友好性：由于数组的数据在内存中是连续存储的，这使得它在访问时具有良好的缓存友好性。现代处理器的缓存机制可以显著加快数组的访问速度，尤其是当遍历数组时，连续的内存访问可以充分利用缓存，提高程序的整体性能。
数组的初始化：在某些编程语言中，未初始化的数组元素可能会含有不确定的值，这可能导致不可预测的程序行为。因此，最好在数组创建时就初始化所有元素，以避免意外的错误。
静态数组与动态数组：静态数组的大小在编译时确定，而动态数组的大小可以在运行时根据需要进行调整。对于需要灵活大小的应用，动态数组（如 C++ 中的 std::vector 或 Python 中的列表）更为合适，但也要注意动态调整大小时可能带来的性能开销。

1.3 数组的优点与局限性

数组存储在连续的内存空间内，且元素类型相同。这种设计具有明显的优势，因为系统可以利用这些先验信息来优化操作效率。

空间效率高：数组分配了连续的内存块，不需要额外的结构性开销。
支持随机访问：数组允许在 (O(1)) 时间内直接访问任意元素。
缓存局部性好：当访问数组元素时，计算机会将其附近的其他数据也加载到缓存中，从而利用高速缓存提高后续操作的执行速度。

然而，连续内存存储也有其局限性：

插入与删除效率低：当数组中元素较多时，插入或删除操作可能需要移动大量元素，导致操作效率降低。
长度不可变：数组在初始化时长度就已固定，若需扩容则必须将所有数据复制到新数组中，这会产生较大的开销。
可能导致空间浪费：如果数组分配的大小超过实际需求，未使用的空间将被浪费。

1.4 数组的典型应用

数组作为一种基础且常见的数据结构，广泛应用于各种算法中，并可用于实现多种复杂的数据结构。

随机访问：数组适合用于存储需要随机抽样的数据。通过生成随机序列并利用索引，可以轻松实现随机抽样。
排序和搜索：数组是排序和搜索算法中最常用的数据结构。例如，快速排序、归并排序、二分查找等算法通常基于数组进行操作。
查找表：当需要快速查找元素或其对应关系时，数组可以用作查找表。例如，要实现字符到 ASCII 码的映射，可以将字符的 ASCII 码值作为数组的索引，并在对应位置存放相应的元素。
机器学习：在神经网络中，大量的线性代数运算涉及向量、矩阵和张量，这些数据结构通常以数组形式构建。数组是神经网络编程中最常用的数据结构之一。
数据结构实现：数组可以用于实现栈、队列、哈希表、堆、图等数据结构。例如，图的邻接矩阵表示实际上是一个二维数组。

2. 数组常用操作（python）

2.1 初始化数组

Python 中的数组可以通过列表来初始化。列表是 Python 中的一种内置数据类型，可以用来表示数组。

# 初始化一个空数组
arr = []

# 初始化一个有默认值的数组
arr = [1, 2, 3, 4, 5]

2.2 访问元素

数组元素被存储在连续的内存空间中，这意味着计算数组元素的内存地址非常容易。给定数组内存地址（首元素内存地址）和某个元素的索引，我们可以使用下图所示的公式计算得到该元素的内存地址，从而直接访问该元素。

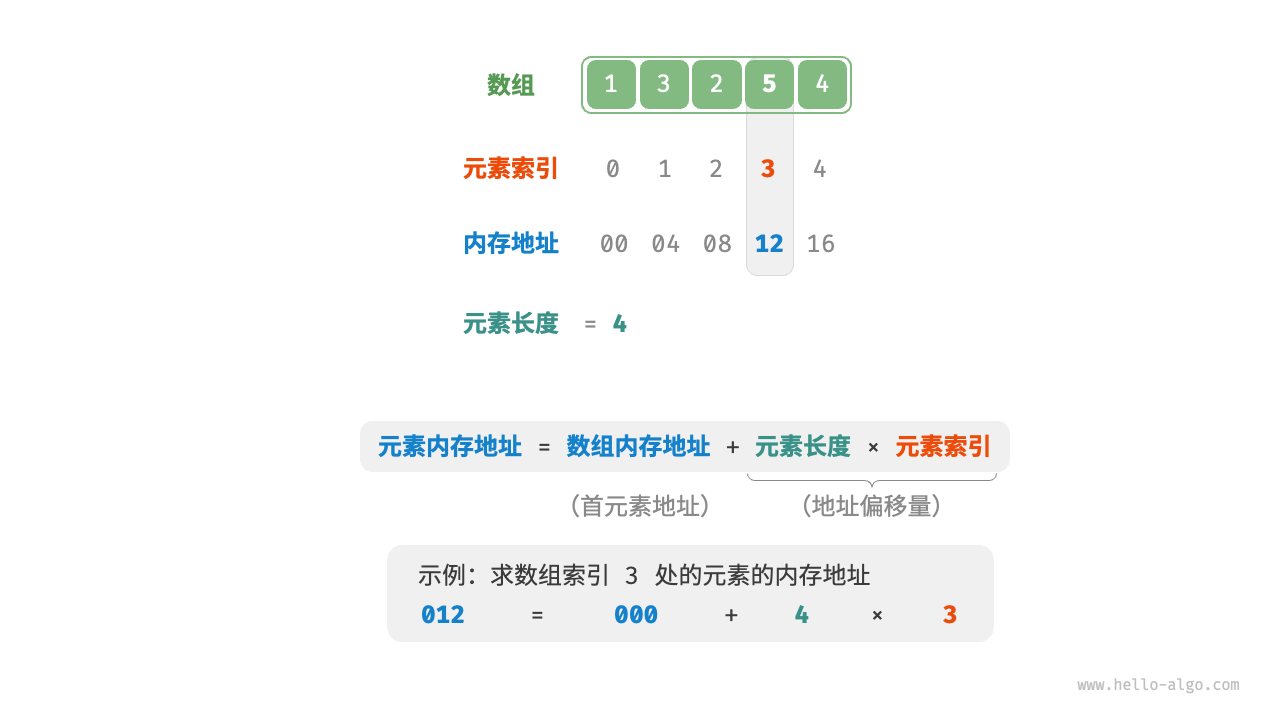
我们发现数组首个元素的索引为0，这似乎有些反直觉，因为从1开始计数会更自然。但从地址计算公式的角度看，索引本质上是内存地址的偏移量。首个元素的地址偏移量是0，因此它的索引为0是合理的。在数组中访问元素非常高效，我们可以在$O(n)$时间内随机访问数组中的任意一个元素。

arr = [1, 2, 3, 4, 5]

# 访问第一个元素
print(arr[0])  # 输出：1

# 访问最后一个元素
print(arr[-1])  # 输出：5

# 在区间 [0, len(nums)-1] 中随机抽取一个数字
random_index = random.randint(0, len(nums) - 1)
# 获取并返回随机元素
random_num = nums[random_index]

2.3 插入元素

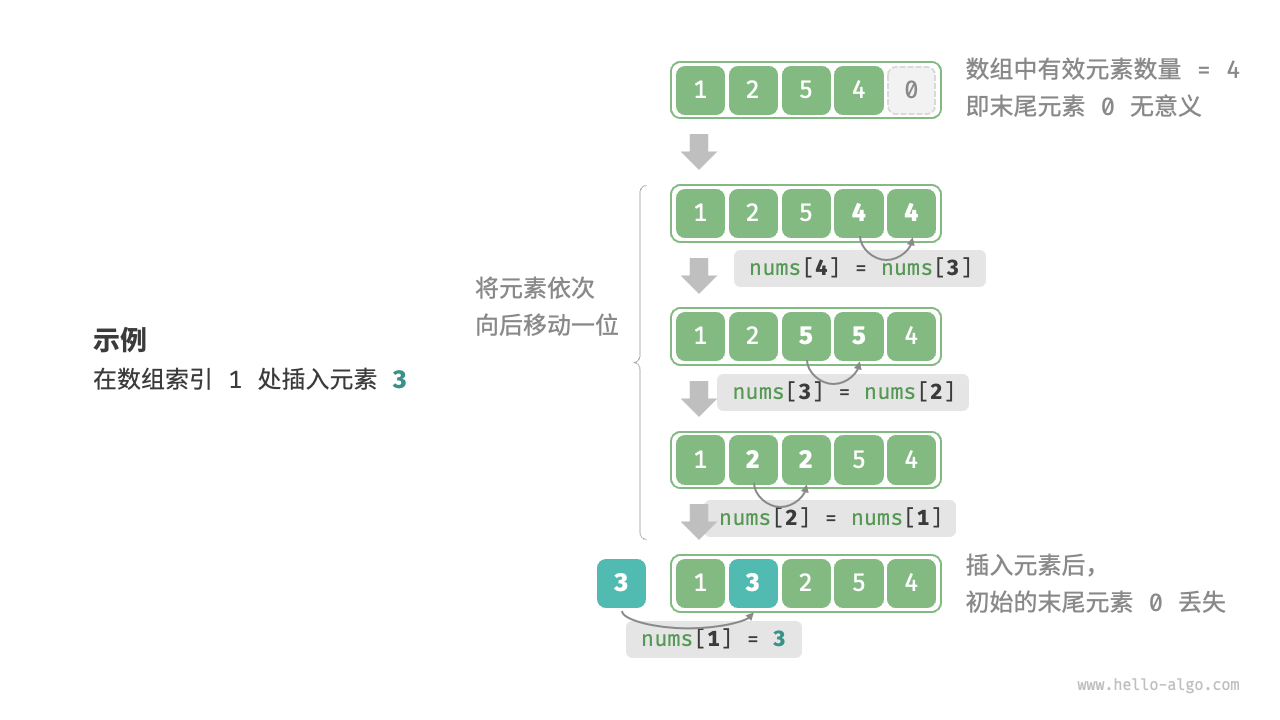
数组元素在内存中是“紧挨着的”，它们之间没有空间再存放任何数据。如图 4-3 所示，如果想在数组中间插入一个元素，则需要将该元素之后的所有元素都向后移动一位，之后再把元素赋值给该索引。

arr = [1, 2, 3, 4, 5]

# 在数组末尾插入一个元素
arr.append(6)
print(arr)  # 输出：[1, 2, 3, 4, 5, 6]

# 在索引为2的位置插入元素
arr.insert(2, 10)
print(arr)  # 输出：[1, 2, 10, 3, 4, 5, 6]

在 Python 中，列表（我们常常将其作为数组使用）是动态数组，因此它们的长度不是固定的。这意味着你可以随意添加或删除元素，列表会自动调整其大小。因此，不会发生由于插入一个元素导致尾部元素“丢失”的情况。

然而，如果你要模拟一种固定长度的数组行为，那么插入新元素时，确实可能需要手动移除尾部元素来保持数组的长度不变。下面是一个例子来展示这种行为：

# 初始化一个固定长度为5的数组
fixed_length_arr = [1, 2, 3, 4, 5]
max_length = 5

# 在固定长度的数组中插入新元素
new_element = 6
if len(fixed_length_arr) >= max_length:
    fixed_length_arr.pop(0)  
# 移除第一个元素，模拟元素向左移动
fixed_length_arr.append(new_element)

print(fixed_length_arr)  # 输出：[2, 3, 4, 5, 6]

在这个例子中，我们通过删除数组的第一个元素来模拟“丢失”效果，从而保持数组的长度不变。当我们插入一个新元素时，数组中的元素向左移动，最左边的元素被移除。

这种操作类似于固定大小的队列（队列中的新元素进入，旧元素离开），可以用于特定的场景，比如实现滚动窗口或有限历史记录的缓存。

2.4 删除元素

可以使用 remove() 方法删除数组中的指定元素，或者使用 pop() 方法删除指定位置的元素。

arr = [1, 2, 3, 4, 5]

# 删除指定值的元素
arr.remove(3)
print(arr)  # 输出：[1, 2, 4, 5]

# 删除索引为1的元素
arr.pop(1)
print(arr)  # 输出：[1, 4, 5]

# 删除数组末尾的元素
arr.pop()
print(arr)  # 输出：[1, 4]

2.5 遍历数组

可以使用 for 循环遍历数组中的元素。

arr = [1, 2, 3, 4, 5]

# 遍历数组
for element in arr:
    print(element)

2.6 查找元素

可以使用 in 关键字判断某个元素是否存在于数组中，也可以使用 index() 方法获取某个元素的索引。

arr = [1, 2, 3, 4, 5]

# 判断元素是否在数组中
if 3 in arr:
    print("3 在数组中")

# 获取某个元素的索引
index = arr.index(4)
print("元素 4 的索引为:", index)

2.7 扩容数组

Python 的列表会根据需要自动扩容。添加新元素时，列表的容量会自动增加。因此不需要手动扩容，但如果你需要模拟扩容的效果，可以通过以下方式实现。

arr = [1, 2, 3]

# 假设数组容量不够，可以通过扩展数组的方式扩容
arr.extend([4, 5, 6])
print(arr)  # 输出：[1, 2, 3, 4, 5, 6]

# 或者使用append逐个添加元素
arr.append(7)
print(arr)  # 输出：[1, 2, 3, 4, 5, 6, 7]

3. 八股文中的数组

3.1 数组与链表的区别是什么？

连续存储 vs. 非连续存储：数组的元素在内存中是连续存储的，而链表的元素可以分散存储。
访问速度：数组可以通过下标随机访问，时间复杂度为 O(1)；而链表访问指定元素需要遍历，时间复杂度为 O(n)。
插入与删除：数组在中间位置插入或删除元素时，需要移动其他元素，时间复杂度为 O(n)；链表在中间插入或删除元素，只需调整指针，时间复杂度为 O(1)。
内存占用：数组需要在初始化时指定大小，且大小固定；链表可以根据需要动态扩展，但每个元素额外占用存储指针的内存。

3.2 如何计算数组中元素的内存地址？

公式：对于一个起始地址为 base_address 的数组，数组中第 i 个元素的内存地址可以通过公式 address = base_address + i * element_size 计算，其中 element_size 是数组中每个元素的字节数。
应用：理解这个公式有助于更好地掌握数组的底层原理，特别是在指针操作、内存布局和优化方面。

3.3 数组的优缺点是什么？

优点：
- 支持快速随机访问，时间复杂度为 O(1)。
- 内存连续性使得数组在缓存命中率和内存局部性上表现良好，适合高性能计算。
缺点：
- 固定大小，无法动态调整，容易出现内存浪费或不足的问题。
- 在插入和删除操作上效率较低，特别是当操作发生在数组中间时。

3.4 什么是动态数组？与静态数组相比有什么优势？

动态数组：如 C++ 中的 std::vector 或 Python 的列表，可以根据需要动态调整大小，通常在容量不足时会以一定倍数扩容。
优势：
- 大小灵活，可以根据需要动态增加或减少元素，避免了内存浪费。
- 尽管在扩容时有一定的性能开销，但一般通过倍增策略来减少扩容次数，从而均摊操作成本。

3.5 解释数组的内存对齐与填充问题。

内存对齐：为了提高内存访问效率，编译器通常会将数组元素按照其数据类型的大小进行对齐。对齐规则可能导致数组元素之间有额外的填充字节，尤其是在多维数组或结构体中使用数组时。
填充：内存对齐可能会在元素之间引入填充字节，以确保下一个元素的地址满足对齐要求。这对高性能计算和嵌入式系统中的内存优化尤为重要。

3.6 多维数组的内存布局是怎样的？

行优先（Row-major）存储：在大多数编程语言中（如 C 和 C++），多维数组按照行优先顺序存储，即先按行存储，再按列存储。
列优先（Column-major）存储：一些语言（如 Fortran）采用列优先存储方式，即先按列存储，再按行存储。
影响：不同的内存布局会影响数组在算法中的遍历效率，理解这些布局有助于优化算法的性能，特别是在科学计算和图像处理领域。

3.7 数组与指针的关系是什么？

指针与数组：在 C 和 C++ 中，数组名可以看作是指向数组第一个元素的指针。数组元素可以通过指针算术来访问。
区别：尽管数组名可以作为指针使用，但数组名是一个常量指针，不能修改指向的地址。而普通指针可以被重新赋值以指向其他内存地址。
应用：理解数组与指针的关系是掌握低级编程技术和优化程序性能的重要基础。

3.8 数组初始化方式有哪些？

静态初始化：在声明数组时同时为其分配值，如 int arr[5] = {1, 2, 3, 4, 5};。
动态初始化：在运行时动态分配数组的大小，并逐个为元素赋值，如 int* arr = new int[n];。
默认初始化：某些语言（如 C++）会将未初始化的数组元素默认赋值为零，而在 C 中未初始化的数组元素则包含不确定的值。

3.9 如何实现数组的逆序？

双指针法：使用两个指针分别指向数组的头尾，交换两个指针所指向的元素，然后移动指针，直到两个指针相遇为止。
时间复杂度：这种方法的时间复杂度为 O(n)，因为每个元素需要访问一次。

3.10 数组与栈的关系是什么？

数组实现栈：栈可以用数组来实现，主要通过一个指针（或索引）来表示栈顶元素的位置。
操作：栈的基本操作如 push 和 pop 可以通过对数组的操作来实现，数组尾部的操作效率较高，时间复杂度为 O(1)。
限制：使用数组实现的栈在初始化时需要确定大小，如果栈深度超过数组大小，则需要进行扩容，或导致栈溢出。

4. 力扣中的数组

4.1 二分查找

力扣题目链接704.二分查找

这道题目的前提是数组为有序数组，同时题目还强调数组中无重复元素，因为一旦有重复元素，使用二分查找法返回的元素下标可能不是唯一的，这些都是使用二分法的前提条件，当大家看到题目描述满足如上条件的时候，可要想一想是不是可以用二分法了。

方法 1: 线性搜索

虽然在有序数组中线性搜索不是最优选择，但它是最简单的搜索方法，时间复杂度为 (O(n))。

def linear_search(nums, target):
    for i in range(len(nums)):
        if nums[i] == target:
            return i
    return -1

方法 2: 二分查找（正常实现）

你可以使用二分查找来实现这个问题。二分查找的时间复杂度为 (O(\log n))，非常适合在有序数组中查找目标值。下面是一个简单的 Python 实现：

def search(nums, target):
    left, right = 0, len(nums) - 1
    
    while left <= right:
        mid = (left + right) // 2
        
        if nums[mid] == target:
            return mid
        elif nums[mid] < target:
            left = mid + 1
        else:
            right = mid - 1
    
    return -1

方法 3: 二分查找（递归实现）

之前的二分查找是迭代实现的，下面是递归实现的版本。

def binary_search_recursive(nums, target, left, right):
    if left > right:
        return -1
    
    mid = (left + right) // 2
    
    if nums[mid] == target:
        return mid
    elif nums[mid] < target:
        return binary_search_recursive(nums, target, mid + 1, right)
    else:
        return binary_search_recursive(nums, target, left, mid - 1)

def search_recursive(nums, target):
    return binary_search_recursive(nums, target, 0, len(nums) - 1)

方法 4: 插值查找

插值查找是一种改进的二分查找，适用于数据分布均匀的数组。时间复杂度在最坏情况下仍然是 (O(\log n))，但在最佳情况下可以接近 (O(\log \log n))。

def interpolation_search(nums, target):
    low = 0
    high = len(nums) - 1
    
    while low <= high and target >= nums[low] and target <= nums[high]:
        # 插值公式
        pos = low + ((target - nums[low]) * (high - low)) // (nums[high] - nums[low])
        
        if nums[pos] == target:
            return pos
        if nums[pos] < target:
            low = pos + 1
        else:
            high = pos - 1
    
    return -1

4.2 移除元素

力扣题目链接27. 移除元素

算法与数据结构 (Algorithms and Data Structures)

数组(3)